Частотные критерии устойчивости САУ
Это графоаналитические методы, позволяющие по виду частотных характеристик САУ судить об их устойчивости. Их общее достоинство в простой геометрической интерпретации, наглядности и в отсутствии ограничений на порядок дифференциального уравнения. Запишем характеристическое уравнение САУ в виде
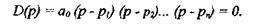
Его корни
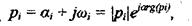
где

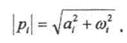
Каждый корень можно изобразить вектором на комплексной плоскости (рис.6.13а), тогда разность р - рi изобразится разностью векторов (рис.6.13б), где р - любое число.
Если менять значение р произвольным образом, то конец вектора р - pi будет перемещаться по комплексной плоскости, а его начало будет оставаться неподвижным, так как рi - это конкретное неизменное значение.
В частном случае, если на вход системы подавать гармонические колебания с различной частотой ω, то р = jω, а характеристическое уравнение принимает вид:
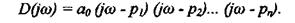
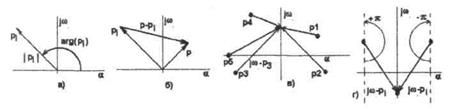
Рисунок 6.13 - К определению корней характеристического уравнения на комплексной плоскости.
При этом концы векторов jω- pi будут находиться на мнимой оси (рис.6.13в). Если менять ωот -∞ до +∞, то каждый вектор jω -pi будет поворачиваться относительно своего начала рi на угол +р для левых и - р для правых корней (рис.6.13г).
Характеристическое уравнение можно представить в виде
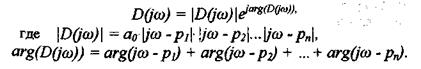
Пусть из n корней m - правые, а (n - m) - левые, тогда угол поворота вектора D(jω) при изменении ω от -∞ до +∞ равен
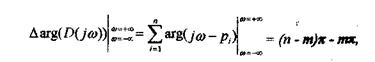
или при изменении со от О д0 +ет получаем
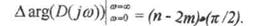
изменение аргумента вектора D(jω) при изменении частоты ω от -∞ до +∞ равно разности между числом левых и правых корней уравнения D(p) = 0, умноженному на π, а при изменении частоты ω от 0 до +∞ эта разность умножается на π/2.
Это правило называется принцип аргумента Он положен в основе всех частотных критериев устойчивости.
Мы рассмотрим два наиболее распространенных критерия: критерий Михайлова и критерий Найквиста.
Критерий устойчивости Михайлова. Так как для устойчивой САУ число правых корней m=0, то угол поворота вектора D(jω) составит

САУ будет устойчива, если вектор D(j ω) при изменении частоты ω от 0 до +∞ повернется на угол п π/2.
При этом конец вектора опишет кривую, называемую годографом Михайлова. Она начинается на положительной полуоси, так как D(0) =аn и последовательно проходит против часовой стрелки n квадрантов комплексной плоскости, уходит в бесконечность в n-ом квадранте (рис.6.14а).
Если это правило нарушается (например, число проходимых кривой квадрантов не равно n, или нарушается последовательность прохождения квадрантов (рис.6.14б), то такая САУ неустойчива - это и есть необходимое и достаточное условие критерия Михайлова. Этот критерий удобен своей наглядностью. Так, если кривая проходит вблизи начала координат, то САУ находится вблизи границы устойчивости и наоборот. Этим критерием удобно пользоваться, если известно уравнение замкнутой САУ.
Для облегчения построения годографа Михайлова выражение для D(jg>) представляют суммой вещественной и мнимой составляющих:

Меняя ω от 0 до ∞, по этим формулам находят координаты точек годографа, которые соединяют плавной линией.
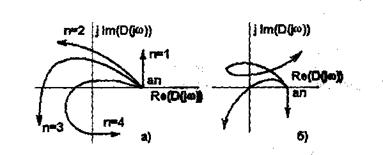
Рисунок 6.14 - Годограф Михайлова.
Критерий устойчивости Найквиста. Этот критерий позволяет судить об устойчивости замкнутой САУ по виду АФЧХ разомкнутой САУ (рис.6.15). Исследование разомкнутой САУ проще, чем замкнутой. Его можно производить экспериментально, поэтому часто оказывается, что АФЧХ разомкнутой САУ мы имеем или можем получить.
Передаточная функция разомкнутой САУ:
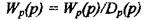
| и ее уравнение динамики: |
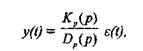
или

где Dp(p) - характеристическое уравнение разомкнутой САУ;
Кр(р)- операторный коэффициент передачи разомкнутой САУ;
ε(t)- рассогласование на входе разомкнутой САУ.
По виду корней уравнения Dp(p) = 0 можно судить об устойчивости разомкнутой САУ. Но это пока ничего не говорит об устойчивости замкнутой САУ.
Для того, чтобы получить уравнение динамики замкнутой САУ при свободном движении, считаем, что внешнее воздействие u = 0, тогда на вход первого звена САУ подается сигнал рассогласования
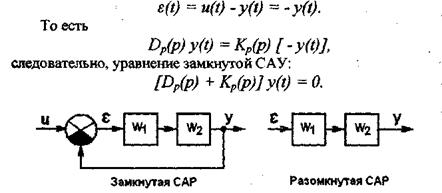
Рисунок 6.15 - К использованию критерия устойчивости Найквиста.
Таким образом, характеристическое уравнение замкнутой САУ:

По виду его корней уже можно судить об устойчивости замкнутой САУ.
Воспользуемся вспомогательной функцией:
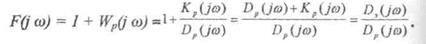
По сути дела она представляет собой АФЧХ разомкнутой САУ, сдвинутую на единицу вправо. Степени полиномов D3(ω) и Dp(jω) равны n. Эти полиномы имеют свои корни рзi и ppi, то есть можно записать
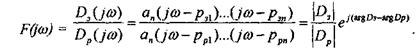
Каждую разность в скобках можно представить вектором на комплексной плоскости, конец которого скользит по мнимой оси ω. При изменении ω от -∞ до +∞ каждый из векторов jω - pi будет поворачиваться на угол +р, если корень левый и -р, если корень правый.
Пусть полином D3(jω) имеет т правых корней и п - т левых, а полином Dp(jω) имеет g правых корней и n-g левых. Тогда суммарный угол поворота вектора функции F(jω) при изменении частоты ω от -∞ до +∞:
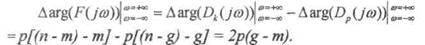
Если замкнутая САУ устойчива, то т = 0, тогда суммарный поворот вектора F(jω) при изменении ω от -∞ до +∞ должен быть равен 2π g, а при изменении ω от 0 до +∞ он составит
2π g/2.
Отсюда можно сформулировать критерий устойчивости Найквиста: если разомкнутая САУ неустойчива и имеет g правых корней, то для того чтобы замкнутая САУ была устойчива, необходимо и достаточно, чтобы вектор F(fω) при изменении ω от 0 до +∞ охватывал начало координат в положительном направлении g/2 раз, то есть АФЧХ разомкнутой САУ должна охватывать g/2 раз точку (-1, j0).
На рис.6.16а приведены АФЧХ разомкнутых САУ, устойчивых в замкнутом состоянии, на рис. 6.16б - замкнутая САУ неустойчива.
На рис. 6.16в и 6.16г показаны АФЧХ разомкнутых астатических САУ, соответственно устойчивых и неустойчивых в замкнутом состоянии. Их особенность в том, что АФЧХ при ω→0 уходит в бесконечность
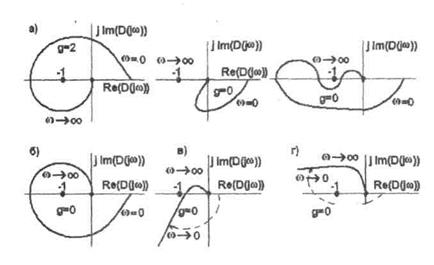
Рисунок 6.16- Применение критерия Найквиста для анализа устойчивости разомкнутых и замкнутых САУ.
В этом случае при использовании критерия Найквиста ее мысленно замыкают на вещественную ось по дуге окружности бесконечно большого радиуса. Критерий Найквиста очень нагляден. Он позволяет не только выявить, устойчива ли САУ, но и, в случае, если она неустойчива, наметить меры по достижению устойчивости.
Дата добавления: 2015-04-21; просмотров: 1234;
