Основные условия устойчивости

Можно провести аналогию между САУ и пружиной, колеба­ния которой описываются аналогичным дифференциальным уравнением (рис.6.9).

В соответствии с классическим методом решение дифферен­циального уравнения ищется в виде:

y(t)= y_вын(t)+ y_св(t)

где - y_cв(t) - общее решение однородного дифференциального уравнения, то есть уравнения с нулевой правой частью:

а₀y_(п) + а₁у_(n-1) + … + а_(n-1) y΄+a_ny = 0;

где - y_вын(t) - частное решение неоднородного дифференциаль­ного уравнения, под которым понимается уравнение с ненулевой правой частью

Рисунок 6.9 - Колебание пружины.

Для общего решения неоднородного дифференциального уравнения y_ce(t), когда все внешние воздействия сняты и система абсолютно свободна, ее движения опреде­ляются лишь собственной структурой. По­этому решение данного уравнения называет­ся свободной составляющей общего реше­ния.

Для частного решения неоднородного дифференциального уравнения y_вын(t) к системе приложено внешнее воздействие u(t). Поэтому вторая со­ставляющая общего решения называется вынужденной. Она оп­ределяет вынужденный установившийся режим работы системы после окончания переходного процесса.

Оттянем пружину, а затем отпустим, предоставив ее самой себе. Пружина будет колебаться в соответствии со свободной со­ставляющей решения уравнения, то есть характер колебаний бу­дет определяться только структурой самой пружины. Если в мо­мент времени t = 0 подвесить к пружине груз, то на свободные колебания наложится внешняя сила Р. После затухания колеба- ний, описываемых только свободной составляющей общего ре­шения, система перейдет в новый установившийся режим, харак­теризуемый вынужденной составляющей с начальным положени­ем У_о и конечным У∞, рис. 6.9.

y_вын(t)=y(t→∞)

Если внешнее воздействие само будет изменяться по сину­соидальному закону Р = P₀sin(ωt+φ), то после затухания пере­ходного процесса система будет совершать вынужденные коле­бания с той же частотой, что и вынуждающая сила, то есть

y_вын = y_maxsin(ωt+φ))

Каждая составляющая общего решения уравнения динамики ищется отдельно.

Вынужденная составляющая ищется на основе решения уравнения статики для данной системы для времени t

Свободная составляющая представляет собой сумму из n от­дельных составляющих:

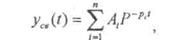
где р_i корни характеристического уравнения

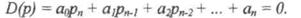
Корни могут быть либо вещественными p_i = а_i, либо попарно комплексно сопряженными

p_i = а_i ±jω_i . Постоянные интегрирования А_i определяются исходя из начальных и конечных условий, подставляя в общее решение значения u, y и их производные в моменты времени t= 0 и t→∞.

Каждому отрицательному вещественному корню соответст­вует экспоненциально затухающая во времени составляющая y_ce(t)_i каждому положительному - экспоненциально расходящая­ся, каждому нулевому корню соответствует y_ce(t)_i ⁼ const (рис.6.10.).

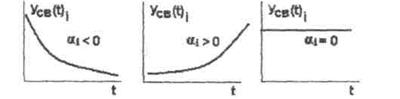
Рисунок 6.10 - Соответствие корней характеристического уровня и изме­нение y_св(t) свободной составляющей

Пара комплексно сопряженных корней с отрицательной ве­щественной частью определяет затухающие колебания с частотой ω_i (рис. 6.11а), при положительной вещественной части (6.116) -расходящиеся колебания, при нулевой - незатухающие (рис.6.11в).

Так как после снятия возмущения y_вын(t) = 0, то устойчивость системы определяется только характером свободной составляю­щей y_св(t). Поэтому условие устойчивости систем по Ляпунову формулируется так: в устойчивой системе свободная состав­ляющая решения уравнения динамики, записанному в отклонени­ях, должна стремиться к нулю, то есть затухать.

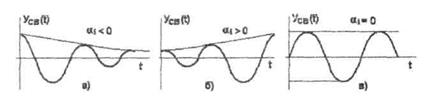
Рисунок 6.11 — Характер колебаний при комплексно сопряженных корнях.

Исходя из расположения на комплексной плоскости корни с отрицательными вещественными частями называются левыми, с положительными - правыми (рис.6.12.).

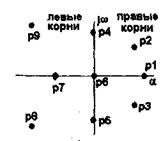
Рисунок 6.12 - Расположение корней харак­теристического уравнения.

Поэтому условие устойчивости ли­нейной САУ можно сформулировать следующим образом: для того, чтобы система была устойчива, необходимо и достаточно, чтобы все корни ее ха­рактеристического уравнения были левыми.

Если хотя бы один корень правый, то система неустойчива. Если один из корней равен нулю (в системах, где а_n=0), а ос­тальные левые, то система находится на границе апериодической устойчивости.

Если равны нулю вещественные части одной или нескольких пар комплексно сопряженных корней, то система находится на границе колебательной устойчивости.

Правила, позволяющие судить о знаках корней характеристи­ческого уравнения без его решения, называются критериями ус­тойчивости. Их можно разделить на алгебраические (основаны на составлении по данному характеристическому уравнению по определенным правилам алгебраических выражений) и частот­ные (основаны на исследовании частотных характеристик).

Если система представлена в виде передаточной функции, то для анализа устойчивости используется ее собственный оператор (знаменатель передаточной фикции).

Полученные корни характеристического уравнения могут быть представлены в виде точек на комплексной плоскости

Для устойчивых систем необходимо и достаточно, чтобы все корни характеристического уравнения лежали слева от мнимой оси комплексной плоскости.

Если хотя бы один вещественный корень или пара комплекс­ных сопряженных корней находится справа от мнимый оси, то система является неустойчивой.

Если имеется нулевой корень или пара чисто мнимых корней, то система считается нейтральной (находящейся на границе ус­тойчивости и неустойчивости). Таким образом, мнимая ось ком­плексной плоскости является границей устойчивости.

С целью упрощения анализа устойчивости систем разработан ряд специальных методов, которые получили название критерии устойчивости.

Критерии устойчивости делятся на две разновидности: алгеб­раические и частотные.

Алгебраические критерии являются аналитическими, а час­тотные - графоаналитическими. Критерии устойчивости позво­ляют оценить влияние параметров системы на ее устойчивость.

Необходимое условие устойчивости.

Характеристическое уравнение системы с помощью теоремы Виета может быть записано в виде

где pi, p₂,..., р„ - корни этого уравнения.

Если система устойчива, значит все корни левые, то есть ве­щественные части всех корней отрицательны, что можно запи­сать как а_i = -| а_i | < 0. Подставим их в уравнение:

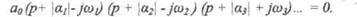
Так как в скобках нет ни одного отрицательного числа, то ни один из коэффициентов а_iне будет отрицательным.

Поэтому необходимым условием устойчивости САУ является положительность всех коэффициентов характеристического уравнения: а_i>0. В дальнейшем будем рассматривать только уравнения, где а₀>0. В противном случае уравнение умножается на-1.

Рассмотренное условие является необходимым, но недоста­точным условием. Необходимые и достаточные условия дают ал­гебраические критерии Рауса и Гурвица,

Раус предложил критерий устойчивости САУ в виде алго­ритма, по которому заполняется специальная таблица с использо­ванием коэффициентов характеристического уравнения:

1) в первой строке записываются коэффициенты уравнения с четными индексами в порядке их возрастания;

2) во второй строке - с нечетными;

3) остальные элементы таблицы определяется по формуле:

c_k,i=c_k+1,i-2-r_ic_k+1,i-1

где r_i = c_1,i-2/c_1,i-1, i ≥ - номер строки, к - номер столбца.

4) число строк таблицы Рауса на единицу больше порядка ха­рактеристического уравнения.

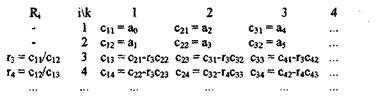
Критерий Рауса: для того, чтобы САУ была устойчива, не­обходимо и достаточно, чтобы коэффициенты первого столбца таблицы Рауса С₁₁, С₁₂, С₁₃,... были положительными.

Если это не выполняется, то система неустойчива, а количе­ство правых корней равно числу перемен знака в первом столбце.

Достоинство данного критерия в том, что он прост в исполь­зовании независимо от порядка характеристического уравнения. Он удобен для использования на ЭВМ. Его недостаток - малая наглядность, трудно судить о степени устойчивости системы, на­сколько далеко отстоит она от границы устойчивости.

Критерий Гурвица. Гурвиц предложил другой критерий ус­тойчивости. Из коэффициентов характеристического уравнения строится определитель Гурвица

по алгоритму:

1) по главной диагонали слева направо выставляются все ко­эффициенты характеристического уравнения от ai до а„;

2) от каждого элемента диагонали вверх и вниз достраивают­ся столбцы определителя так, чтобы индексы убывали сверху вниз;

3) на место коэффициентов с индексами меньше нуля или больше п ставятся нули.

Критерий Гурвица:

для того, чтобы САУ была устойчива, необходимо и доста­точно, чтобы все п диагональных миноров определителя Гурвица были положительны.

Эти миноры называются определителями Гурвица. Рассмот­рим примеры применения критерия Гурвица: 1) n =1 => уравнение динамики:

Определитель Гурвица:

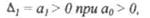
то есть условие устойчивости: а₀ > 0,a₁> 0;

2) п = 2 => уравнение динамики;

а₀p² + а₁p + а₂ = 0.

Определители Гурвица:

∆₁= a₁ > 0, ∆₂ = a₁a₂-a₀a₃ = а₁а₂ > О, так как а₃ = 0, то есть условие устойчивости:

a₀ > 0, a₁ > 0, а₂ > 0;

3) п = 3 => уравнение динамики:

а₀p³ + а₁p² + а₂ p+ а₃ = 0,

Определители Гурвица:

∆₁= a₁ > 0, ∆₂ = a₁a₂ = a₁a₂-a₀a₃ = а₁а₂ > 0, ∆₃ = a₃∆₂ > 0,

условие устойчивости: а₀ > 0, а₁> 0, а₂ > 0,а₃> 0, a₁a₂ – а₀а₃ > 0.

Таким образом, при п ≤ 2 положительность коэффициентов характеристического уравнения является необходимым и доста­точным условием устойчивости САУ. При п > 2 появляются до­полнительные условия.

Критерий Гурвица применяют при п≤4. При больших по­рядках возрастает число определителей и процесс становится трудоемким.

Недостаток критерия Гурвица - малая наглядность. Достоин­ство - удобен для реализации на ЭВМ. Его часто используют для определения влияния одного из параметров САУ на ее устойчи­вость.

Так равенство нулю главного определителя ∆_n= a_n ∆_n-1 = 0 го­ворит о том, что система находится на границе устойчивости. При этом либо а_n = 0 - при выполнении остальных условий сис­тема находится на границе апериодической устойчивости, либо предпоследний минор ∆_n-1 = 0 - при положительности всех остальных миноров система находится на границе колебательной устойчивости.