Комбинационная логика
В устройствах автоматики с логическими входными сигналами часто необходимо вырабатывать определенные выходные сигналы для их передачи на последующие узлы. При этом различают два класса задач.
В задачах первого класса состояние выхода зависит от комбинации входных сигналов. Эти задачи называются комбинационными и решаются с помощью логических устройств, которые выполняют операции булевой алгебры.
Другой класс задач требует не только формирования комбинации входных сигналов, но также знания их прежнего значения. Для решения таких задач применяют последовательные схемы (цифровые автоматы), имеющие в той или иной форме цифровую память.
Комбинационными устройствами называют логические устройства, не имеющие в своём составе запоминающих ячеек, при этом выходные сигналы зависят от входных, имеющих место только в данный момент времени
Все цифровые устройства оперируют двоичными кодами, т.е. наборами нулей и единиц. Для описания цифровых устройств используется алгебра логики, в которой так же, как и в двоичном кодировании, переменные могут принимать только два значения: 0 или 1. В алгебре логики имеется три элементарных действия: дизъюнкция (ИЛИ), конъюнкция (И) и инверсия (НЕ).
Дизъюнкция, или логическое сложение, осуществляется по следующим правилам:
0 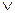 0 =0,
0 =0,
0 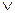 1=1,
1=1,
1 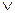 0 = 1,
0 = 1,
1 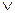 l = 1,
l = 1,
где V - знак операции дизъюнкции.
Можно также пользоваться знаком "+", но в логических выражениях этот знак читается как ИЛИ. В дизъюнкции в отличие от двоичного кодирования при суммировании двух логических единиц переносов не осуществляется.
Конъюнкция, или логическое умножение, осуществляется по следующим правилам:
0 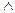 0= 0
0= 0
0 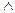 1= 0
1= 0
1 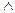 0= 0
0= 0
1 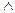 1 =1
1 =1
где 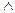 - знак операции конъюнкции. В логических выражениях допустимо также условное изображение операции конъюнкции отсутствием какого либо знака между переменными, записанными без пробела, однако читается это как И.
- знак операции конъюнкции. В логических выражениях допустимо также условное изображение операции конъюнкции отсутствием какого либо знака между переменными, записанными без пробела, однако читается это как И.
Инверсия представляет собой отрицание истины. Например, инверсия единицы есть нуль, а инверсия нуля есть единица. Операция инверсии обозначается прямой чертой над переменной:
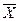 ,
, 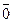 ,
, 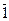
(читается: не-икс, не-нуль, не-единица).
Законы алгебры логики представляют собой комбинации из дизъюнкций, конъюнкций и инверсий над логическими переменными. Возможные соотношения между ними приведены в таблице 8.1.
Законы отрицания в виде функций Пирса и Шеффера являются полными, т.е. посредством этих функций можно описать работу любого, сколь угодно сложного, логического устройства. Число различных логических функций от п переменных определяется соотношением: N =22п.
Дата добавления: 2015-04-21; просмотров: 1373;
