Метод Эйлера

Этот метод является простейшим численным методом решения задачи Коши. Рассмотрим его на примере решения обыкновенного дифференциально­го уравнения первого порядка (6.47) с соответствующим начальным условием (6.48).

Расчетную формулу метода Эйлера можно получить, используя разло­жение функции и(х) в ряд Тейлора в окрестности некоторой точки х_i:

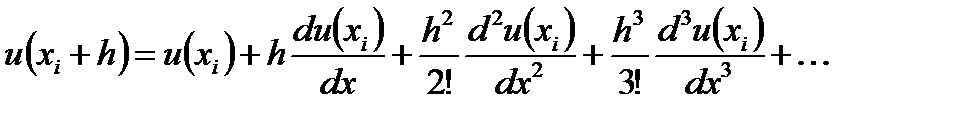(6.49)

Если приращение h мало (то есть h<<x_i), то члены ряда, начиная со слагаемого, включающего h во второй степени, могут быть отброшены как малые величины. Тогда из (6.49) в первом приближении получим:

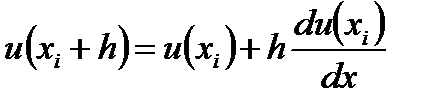(6.50)

Воспользуемся формулой (6.50), применив ее к единственной известной из условия задачи точке x₀. Найдем в х₀ производную du(x₀)/dx, подставив (6.48) в (6.47):

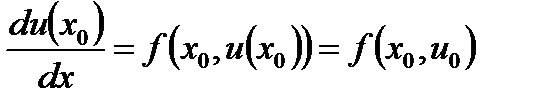
Подставив последнее выражение в (6.50) и полагая x_i = x₀, получим

u (x₀ + h) = u (x₀) + hf (x₀, u (x₀, u (x₀))

или, сокращая обозначения, в окончательном виде

u₁ = u₀ + hf (x₀, u₀)

Таким образом, (6.50) при известном значении функции u₀ = u(x₀) в на­чальной точке x₀ позволяет найти приближенное значение u₁ = u(x₁) при ма­лом смещении h от x₀. На рис. 6.2 графически показан начальный шаг решения методом Эйлера.

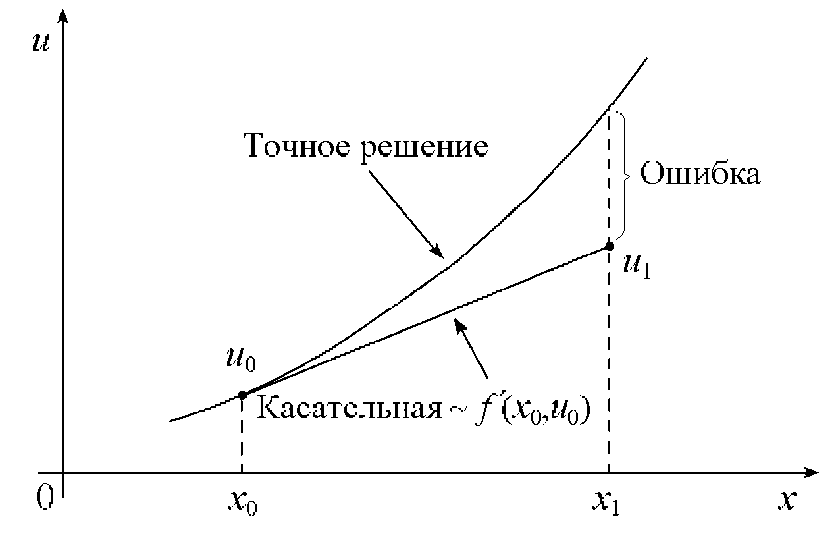
Рис. 6.2 ‑ Метод Эйлера

Решение можно продолжить, используя найденное значение функции u₁ для вычисления следующего значения - u₂. Распространяя эти рассужде­ния на последующие точки, запишем расчетную формулу метода Эйлера в виде

u_i+1 = u_t + hf (x_i, u_i), i = 0,1,2,.... (6.51)

Из рис. 6.1 видно, что ошибка метода Эйлера на шаге связана с исполь­зуемой линейной аппроксимацией u(x). Хотя тангенс угла наклона касатель­ной к кривой точного решения в точке (x₀,u₀) известен и равен du(x₀)/dx, он изменяется при смещении от x₀ до x_i. Следовательно, при сохранении начального наклона касательной на всем интервале h расчет u₁ выполняется с погрешностью.

Ошибка метода Эйлера на каждом шаге имеет порядок h², так как чле­ны, содержащие h во второй и более высоких степенях, отбрасываются - см. (6.49) и (6.50). Уменьшая h можно снизить локальную ошибку на шаге.