Задача Коши
Важным элементом задач, содержащих дифференциальные уравнения, являются дополнительные условия, которые необходимы для получения количественного решения.
Применительно к обыкновенным дифференциальным уравнениям различают два вида задач: задачу с начальными условиями (задачу Коши) и задачу с краевыми условиями (краевую задачу).
Задачу Коши можно сформулировать следующим образом. Дано обыкновенное дифференциальное уравнение
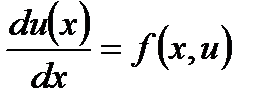(6.47)
и начальное условие
и(хо)= и0 (6.48)
Требуется найти функцию и(х), удовлетворяющую уравнению (6.47) и начальному условию (6.48).
На практике подобные задачи обычно связаны с расчётом переходных электрических, нестационарных тепловых или механических процессов при заданном в некоторый начальный момент времени исходном состоянии системы. Формулировка краевой задачи будет рассмотрена ниже.
Дата добавления: 2015-04-03; просмотров: 839;