Формула трапеций
При п=1 из формулы (6.31) имеем 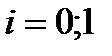 :
:
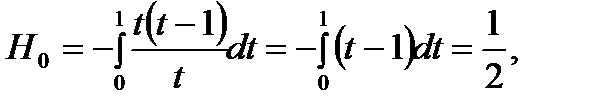
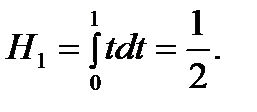
Тогда по формуле (6.32) на отрезке 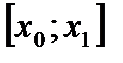 получаем интеграл:
получаем интеграл:
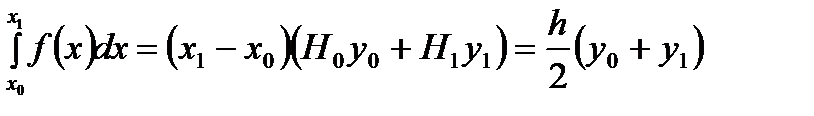 (6.33)
(6.33)
Формула (6.33) дает один из простейших способов вычисления определенного интеграла и называется формулой трапеций. Действительно, при п=1 подынтегральная функция заменяется интерполяционным многочленом Лагранжа первой степени (т.е. линейной функцией), а геометрически это означает, что площадь криволинейной фигуры заменяется площадью трапеции.
Распространяя формулу (6.33) на все отрезки разбиения, получим общую формулу трапеций для отрезка 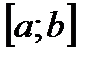 :
:
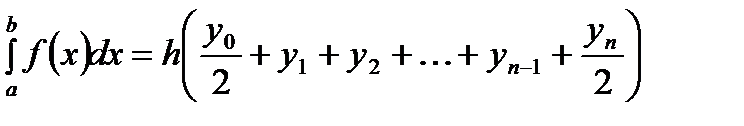 (6.34)
(6.34)
Если аналитическое выражение для подынтегральной функции известно, может быть поставлен вопрос об оценке погрешности численного интегрирования по формуле (6.34) (погрешность метода).
В этом случае имеется ввиду, что
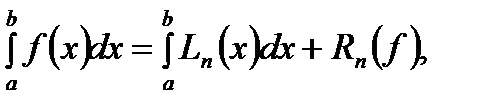
где 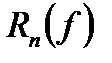 ‑ остаточный член квадратурной формулы (6.34). Формулу остаточного члена получим вначале для отрезка
‑ остаточный член квадратурной формулы (6.34). Формулу остаточного члена получим вначале для отрезка 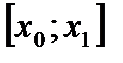 . Имеем:
. Имеем:
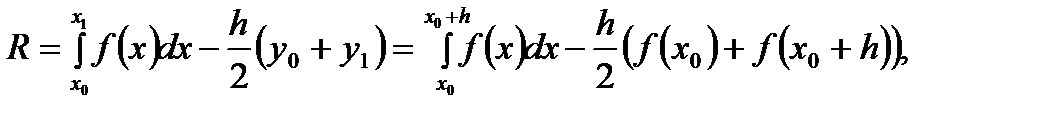
откуда следует, что естественно рассматривать Rкак функцию шага h: R=R(h).Заметим, что R(0)=0.
Продифференцируем R(h) по h:
 Заметим, что
Заметим, что 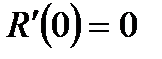 . Далее:
. Далее:
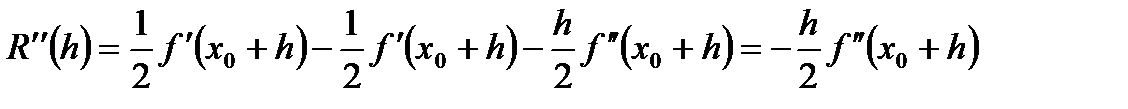 (6.35)
(6.35)
Определим R, последовательно интегрируя 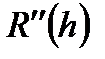 на отрезке
на отрезке 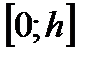 :
:
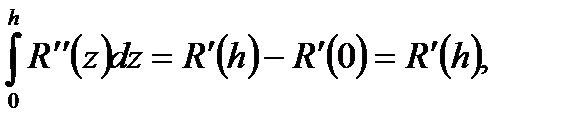
откуда с учетом (6.35) имеем:
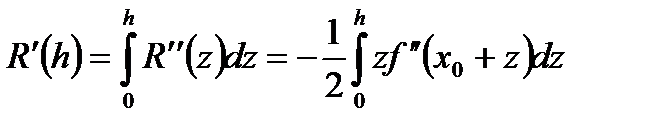 . (6.36)
. (6.36)
Применяя к (6.36) обобщенную теорему о среднем, получаем:
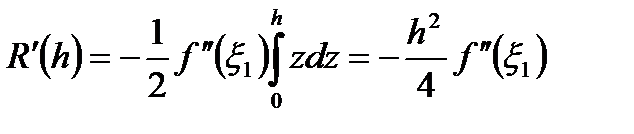 (6.37)
(6.37)
где 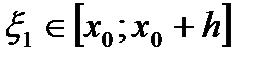 и
и 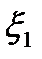 зависит от h. Далее
зависит от h. Далее
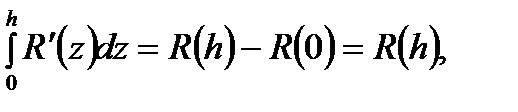 откуда с учетом (6.37) и обобщенной теоремы о среднем имеем:
откуда с учетом (6.37) и обобщенной теоремы о среднем имеем:
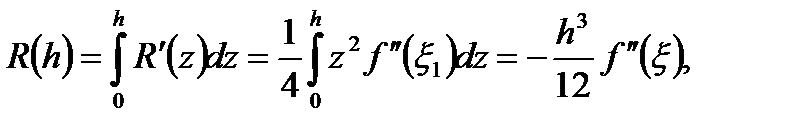
где 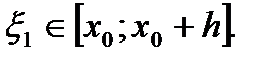
Таким образом, погрешность метода при интегрировании функции на отрезке 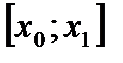 по формуле (6.34) имеет величину:
по формуле (6.34) имеет величину:
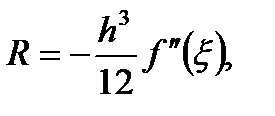
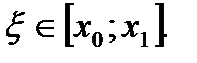 (6.38)
(6.38)
Из формулы (6.38) видно. что при 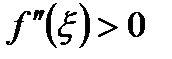 формула (6.34) дает значение интеграла с избытком, а при
формула (6.34) дает значение интеграла с избытком, а при 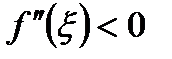 ‑ с недостатком. Можно показать, что при распространении оценки (6.38) на весь отрезок интегрирования
‑ с недостатком. Можно показать, что при распространении оценки (6.38) на весь отрезок интегрирования 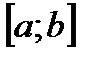 получается формула:
получается формула:
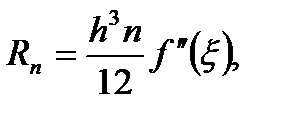
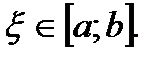
Учитывая, что 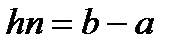 , найден следующий окончательный вид для оценки погрешности метода интегрирования по формуле трапеций:
, найден следующий окончательный вид для оценки погрешности метода интегрирования по формуле трапеций:
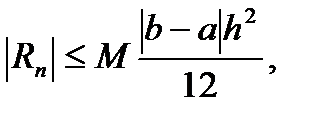 (6.39)
(6.39)
где 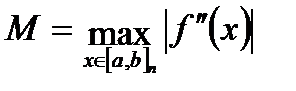 .
.
Пример 6.3.
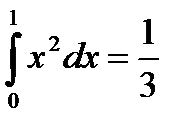
Используем формулу трапеций для n = 2 и n = 4.
Таблица 6.3
| xi | 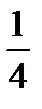
| 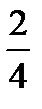
| 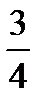
| ||
| f(xi) | 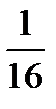
| 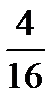
| 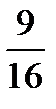
|
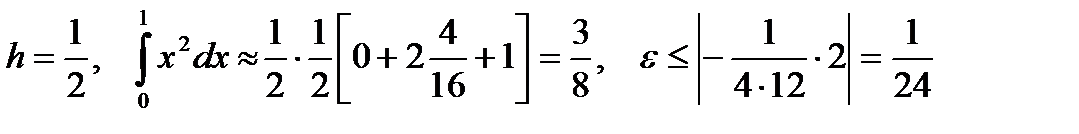
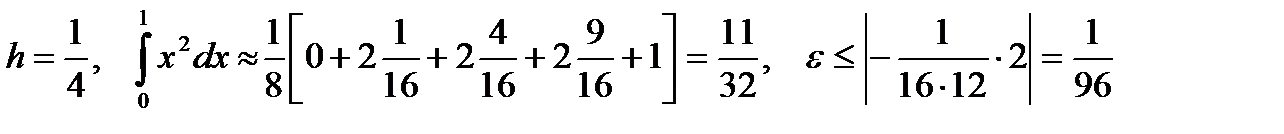
Дата добавления: 2015-04-03; просмотров: 1172;
