Формула Симпсона

При п=2 из формулы (6.31) последовательно имеем (i=0, 1, 2):

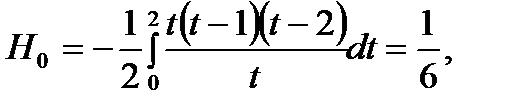
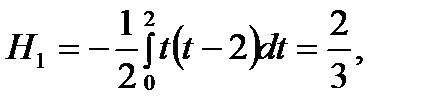
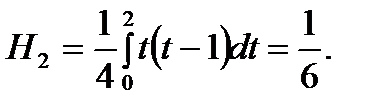
Тогда с учетом (6.32) получим на отрезке :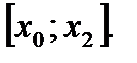

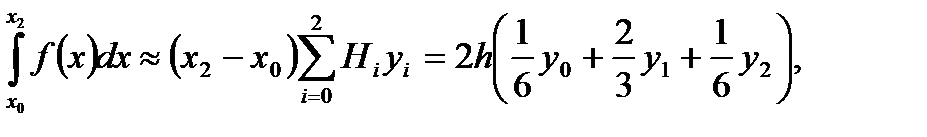
т.е.

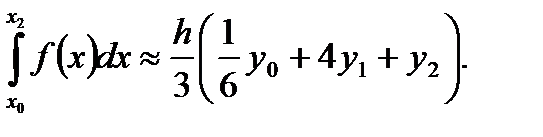(6.40)

Геометрически, в соответствии со смыслом интерполяционной формулы Лагранжа при п=2, использование формулы (5.40) означает замену подынтегральной функции f(x) параболой L₂(x), проходящей через точки M_i(x_i, y_i) (i=0, 1, 2).

Если считать, что п – четное (n=2m), то применяя формулу (6.40) последовательно к каждой паре частичных отрезков 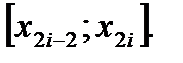(i=1, 2, …, m) получим:

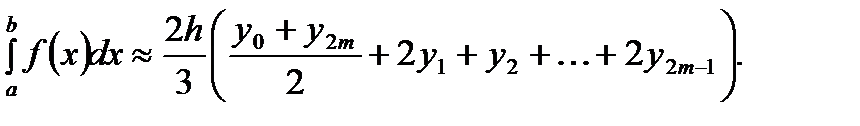(6.41)

Формула (6.41) называется формулой Симпсона.

Оценка остаточного члена формулы Симпсона дается формулой:

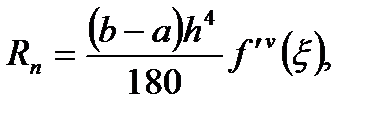
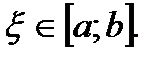
или

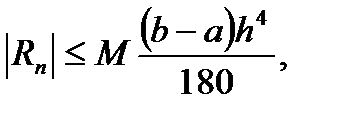(6.42)

где 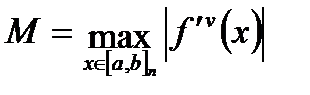. Как следует из оценки, формула Симпсона, оказывается точной для полиномов до третьей степени включительно (т.к. для этих случаев производная четвертого порядка равна нулю). Формула Симпсона обладает повышенной точностью по сравнению с формулой трапеций. Это означает, что для достижения той же точности, что и по формуле трапеций, ней можно брать меньшее число отрезков разбиения.

Укажем простой практический прием позволяющий прогнозировать требуемое число отрезков разбиения по заданной точности .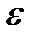

Пусть задана предельная допустимая погрешность интегрирования 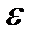Желая иметь 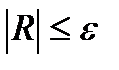с учетом оценки (6.42) достаточно потребовать

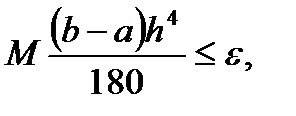
откуда

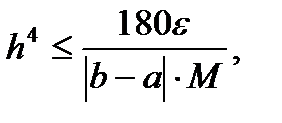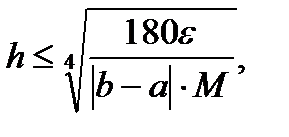т. е. (6.43)

Формула (6.43) позволяет оценить величину шага, необходимую для достижения заданной точности.