Квадратурные формулы Ньютона-Котеса

Применение формулы (6.26) предполагает построение на отрезке интегрирования [a;b] системы узлов интерполяции 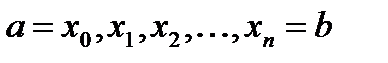, которыми отрезок делится на п частей. Длина 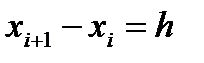, 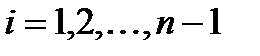называется шагом интегрирования. Естественно считать, что шаг h постоянен, т.е.

.

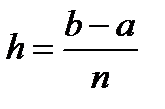В этом случае можно применить интерполяционную формулу Лагранжа для равноотстоящих узлов. Итак, с учетом (6.12) и (6.14) формула (6.28) для весовых коэффициентов A_i примет вид:

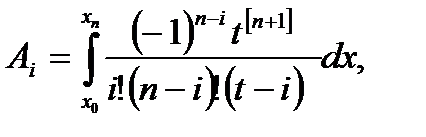
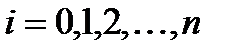(6.29)

Перейдем в этом интеграле к переменной t. Из подстановки (6.9) получаем:

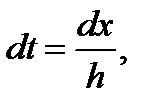т.е.

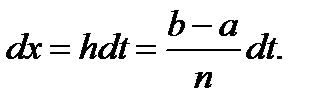
При х=х₀ имеем t=0, а при х=х_nбудет

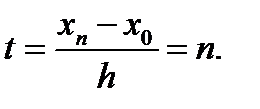
Тогда

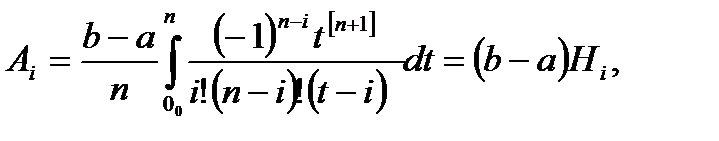(6.30)

где 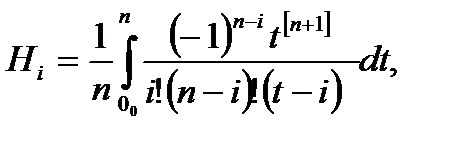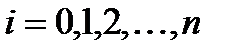(6.31)

Числа (6.29) называют коэффициентами Котеса. Они не зависят от функции f(х), а только от числа точек разбиения. Окончательно, с учетом формул (6.27) и (6.30) получаем следующий вид квуадратурных формул формул Ньютона-Котеса:

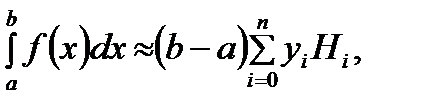(6.32)

дающих на одном участке интегрирования различные представления различного числа п отрезков разбиения.