Приклади розрахунків

Розглянемо приведений вище алгоритм розрахунку різних систем методом сил на конкретних прикладах статично невизначених балок і плоских рам.

Приклад 6.1. Побудувати епюри згинальних моментів для статично невизначеної балки (мал.6.3,а).

а     б   в     г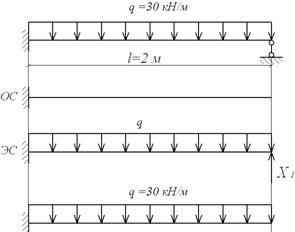

д     е     ж     з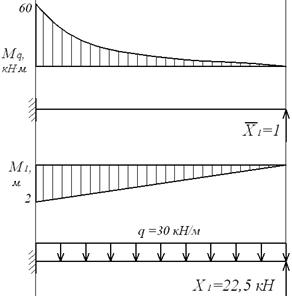

Рис.6.3. До прикладу 6.1

Ступінь статичної невизначеності балки

.

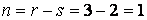Основна й еквівалентна система приведені на мал.6.3,б,в. Такий вибір основної системи є найбільш раціональним, але не єдиним. Можна було, наприклад, замінити жорстке закріплення на шарнірно нерухому опору; тоді основна система представляла б собою статично визначну шарнірну балку, а зайва невідома – зосереджений момент X, прикладений до лівої опори.

Епюра згинальних моментів від зовнішнього навантаження 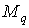(мал.6.3,д) має розмірність кН·м, а одинична епюра моментів 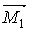(мал.6.3,ж) — м.

Канонічне рівняння методу сил:

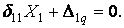
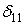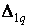Обчислюємо коефіцієнти і , перемножуючи відповідні епюри за правилом Верещагіна:

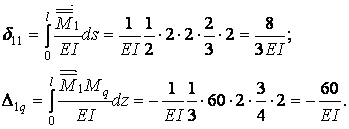
Реакція зайвого зв'язку:

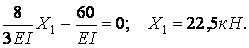
Таким чином, вихідна статично невизначена система, завантажена розподіленим навантаженням q, приведена до статично визначної системи (жорстко затиснена балка), завантаженою розподіленим навантаженням q і зосередженою силою 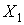(мал.6.3, з).

На мал.6.4,а,б представлені епюри поперечних сил Q 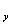і згинальних моментів 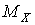для заданої системи.

Відзначимо, що епюри Q 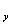і 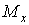(мал.6.4) побудовані безпосередньо методом перетинів, причому за умовами задачі побудова епюри Q 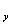не є обов'язковою. Проте, ця епюра дозволила визначити перетин, у якому буде екстремум на епюрі .

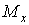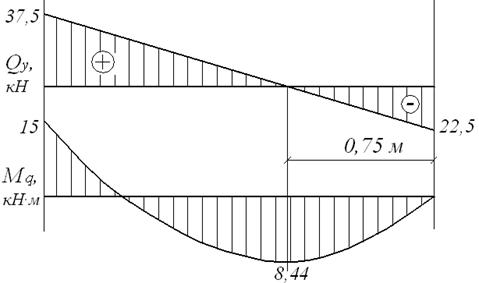
Рис.6.4. Епюри 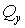і 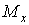для заданої системи

Використання формули (6.8) у виді

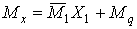
не дає відповіді на питання про місце перебування екстремуму і робить правильну побудову епюри 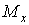більш складною задачею, що вимагає певних навичок.

Приклад 6.2. Побудувати епюри подовжніх, поперечних сил і згинальних моментів для плоскої рами (мал.6.5,а).

Ступінь статичної невизначеності рами:

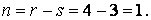
Вибираємо основну систему, відкидаючи на правій опорі горизонтальний стрижень (мал.6.5,б), тобто заміняємо шарнірно-нерухому опору на шарнірно-рухому. На базі основної системи формуємо еквівалентну систему (мал.6.5,в).

Заміняючи реакцію зайвого зв'язку відповідною одиничною силою (мал. 6.5,г), будуємо епюри моментів 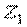(мал.6.5,д).

Вантажна епюра моментів 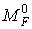(мал.6.5,ж), побудована від одночасної дії всіх зовнішніх навантажень (мал.6.5,е), є знакоперемінною на ділянці, де діє навантаження q. Це створює певні труднощі (хоча і не нездоланні!) при її перемноженні з одиничною епюрю 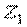. У зв'язку з цим доцільно побудувати дві вантажних епюри — окремо від навантаження q (епюра 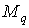) і від спільної дії F і M (епюра 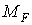). Ці варіанти навантаження і відповідні їм епюри представлені на мал.6.5,з і мал.6.6,а,б,в.

При такій розбивці зовнішнього навантаження канонічне рівняння методу сил містить два вантажних переміщення і має вигляд

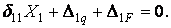
Обчислимо коефіцієнти канонічного рівняння:

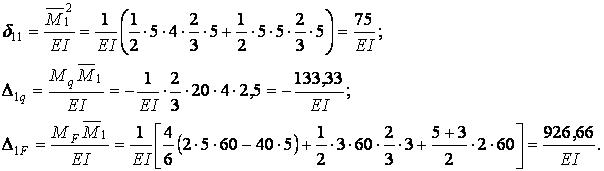
а		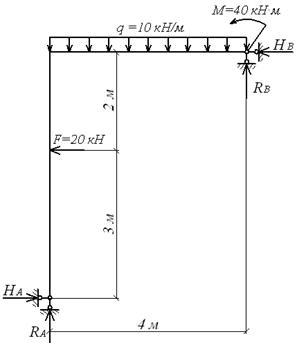б
в		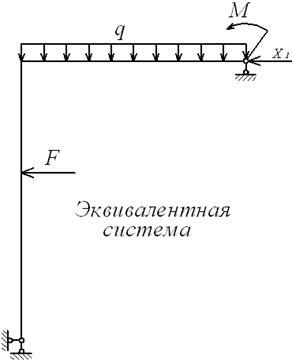г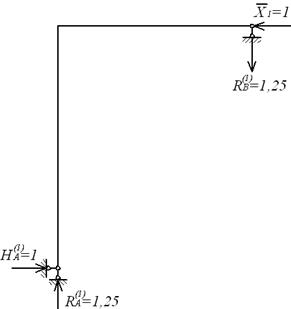
д		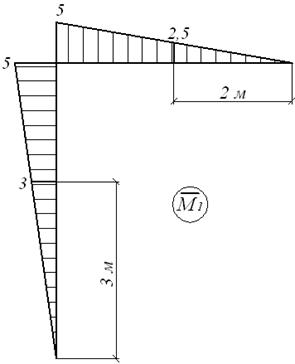е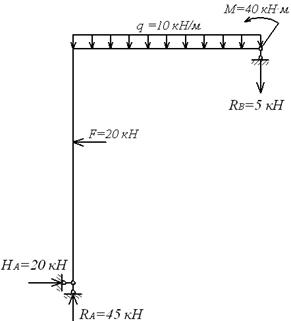
ж		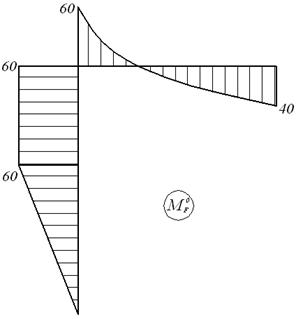з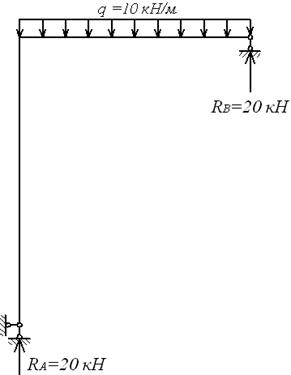

Рис.6.5. До прикладу 6.2

Реакція зайвого зв'язку:

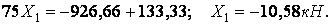
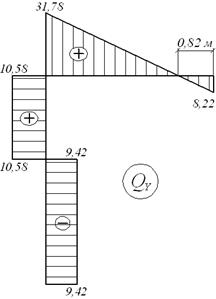
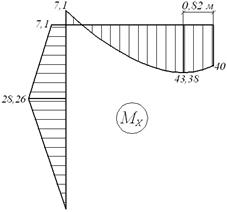
Епюри N_z, Q_y, M_x для заданої системи, завантаженої навантаженнями F, M, q і X₁ (мал.6.6,г) представлені на мал.6.6,д.

а		б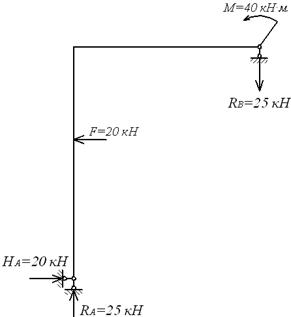
в		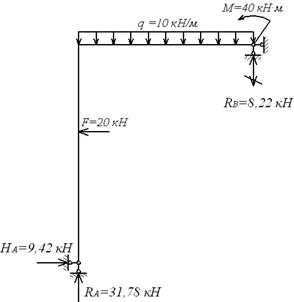г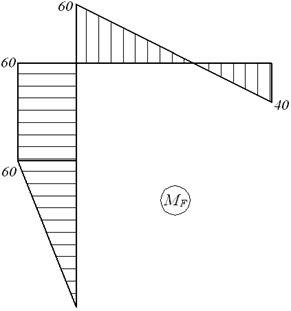
д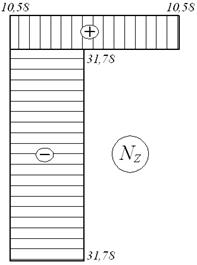

Рис.6.6. До прикладу 6.2 (продовження)

Нагадаємо, що при побудові епюр 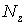і Q_y у рамах ординати можна відкладати в будь-яку сторону, але обов'язково вказувати знаки; а при побудові епюр 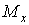знаки можна не вказувати, але обов'язково відкладати ординати з боку розтягнутих волокон відповідних елементів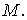

В обох розглянутих прикладах універсальна перевірка правильності обчислення коефіцієнтів канонічного рівняння і вільних членів не виконувалася, тому що балка (приклад 6.1) і рама (приклад 6.2) мають ступінь статичної невизначеності 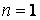, а, виходить, сумарна одинична епюра (якщо її побудувати) збіжиться з одиничною епюрою 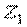. У цьому випадку можна (і бажано!) перевірити правильність виконання розрахунку за допомогою універсальної кінематичної перевірки остаточної епюри моментів .

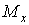Виконаємо цю перевірку для рами, розглянутої в останньому прикладі (мал.6.6,а). Повинна виконуватися умова:

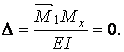
Покажемо окремо фрагменти перемножування епюр (мал.6.6,д і мал.6.6,ж) для ригеля (мал.6.7,а,б) і стійки (мал.6.7,в,г) із вказівкою всіх характерних розмірів і відповідних їм ординат. Причому, стійка (мал.6.7,в,г) повернена в горизонтальне положення.

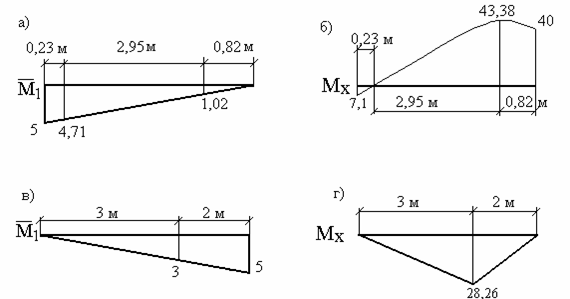
Рис.6.7. Фрагменти перемножування епюр

Точка перетинання кривої на ригелі епюри 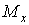з віссю (мал.6.7,б) визначається в такий спосіб. Позначимо координату довільного перетину, відрахуємо від правого кінця ригеля, через z, тоді момент 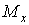визначається у виді

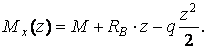
Перетинання з віссю означає, що в цьому перетині 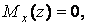тому, підставляючи числові значення, для визначення z при 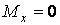одержимо квадратне рівняння

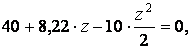
відкіля 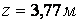(другий корінь цього рівняння позбавлений фізичного змісту).

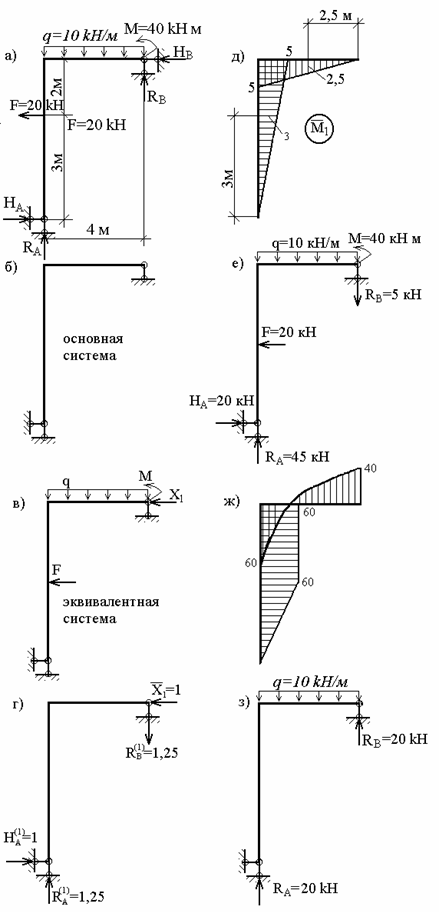
Рис.6.5. До прикладу 6.2

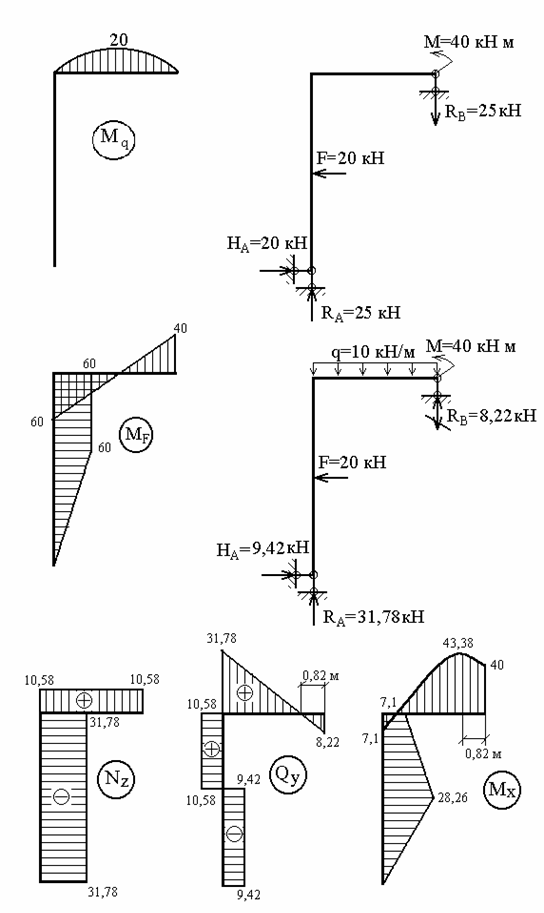
Рис.6.6. Остаточні епюри (до прикладу 6.2)

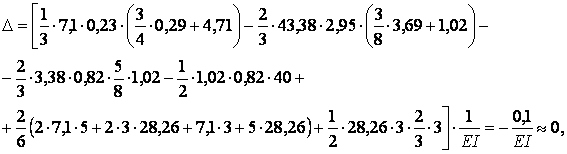
отже, розрахунок виконаний правильно.

Рис.6.7. Фрагменти перемноження епюр (до прикладу 6.2)

Перейдемо до розгляду більш складної системи – рами з двома зайвими зв'язками, для якої алгоритм розрахунку, приведений у параграфі 6.3, можна реалізувати в повному обсязі.

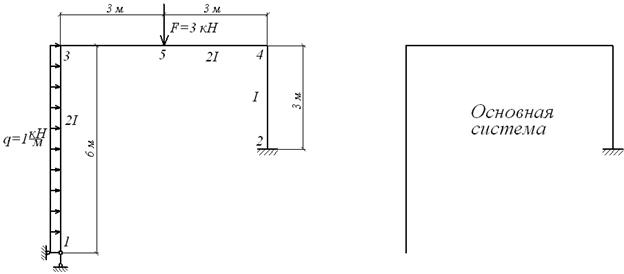
Приклад 6.3. Для рами (мал.6.8,а) побудувати епюри 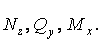Виконати проміжні й остаточні перевірки відповідно до алгоритму розрахунку, зазначеним у параграфі 6.3.

Задана рама має в опорних закріпленнях п'ять зв'язків: два в опорі 1 і три в опорі 2, отже, система двічі статично невизначена:

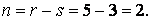
Основну систему доцільно вибрати шляхом видалення шарнірної опори (мал.6.8,б). Відповідна еквівалентна система зображена на мал.6.8,в.

а б

в г

д е

ж з

Рис.6.8. До прикладу 6.3

Система канонічних рівнянь:

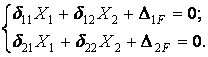
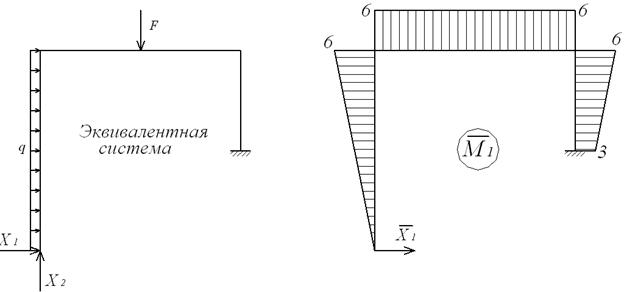
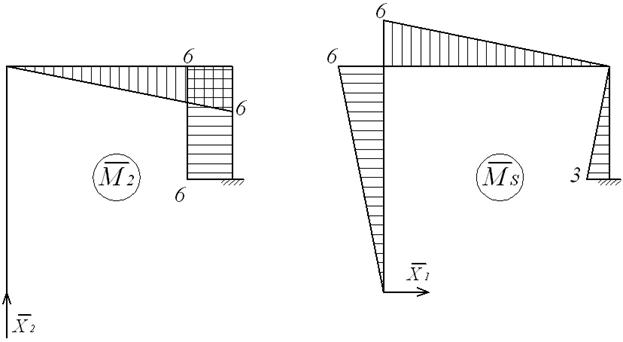
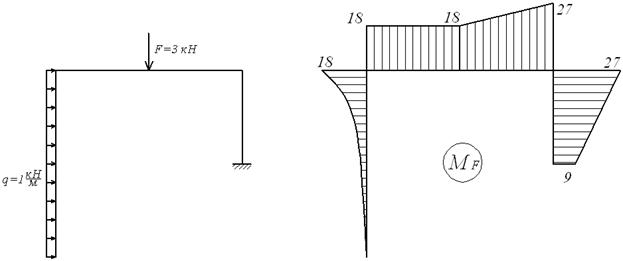
Для обчислення коефіцієнтів і вільних членів канонічних рівнянь будуємо одиничні 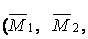мал.6.8,г,д) і вантажну ( 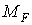, мал.6.8,ж,з) епюри згинальних моментів, а для виконання перевірок — сумарну одиничну епюру 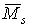(мал.6.8,е).

Коефіцієнти системи канонічних рівнянь обчислюємо шляхом перемноження відповідний епюр за правилом Верещагіна. При цьому обов'язково враховуємо різну жорсткість елементів рами (E2I — на лівій стійці і ригелі; EI — на правій стійці).

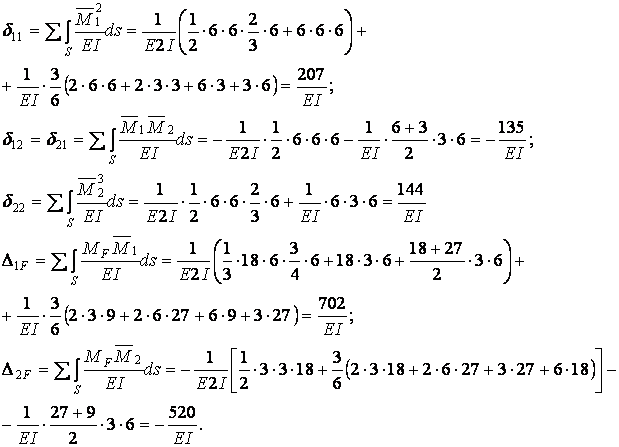
Для перевірки обчислених коефіцієнтів при невідомих і вільних членів канонічних рівнянь використовуємо сумарну одиничну епюру 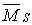(мал.6.8,е).

Повинні виконуватися дві умови:

1)

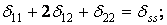
2)

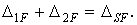
Обчислюємо величини 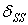і .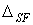

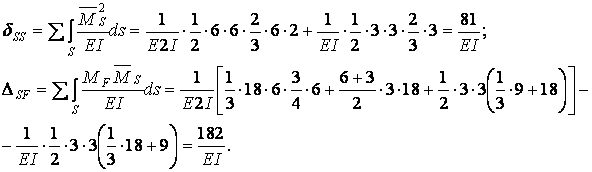
1)

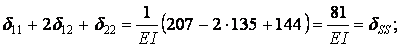
2)

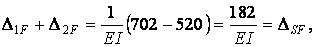
таким чином, коефіцієнти при невідомх і вільні члени канонічних рівнянь обчислені правильно.

Обчислюємо реакції зайвих зв'язків:

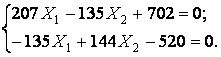
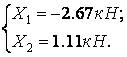
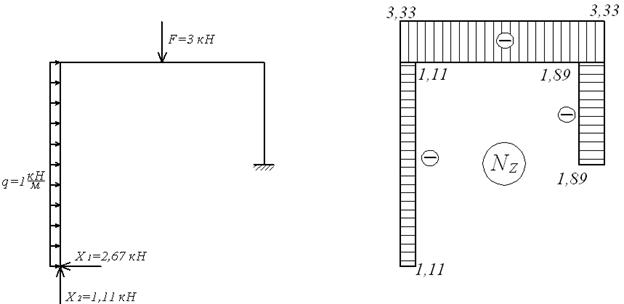
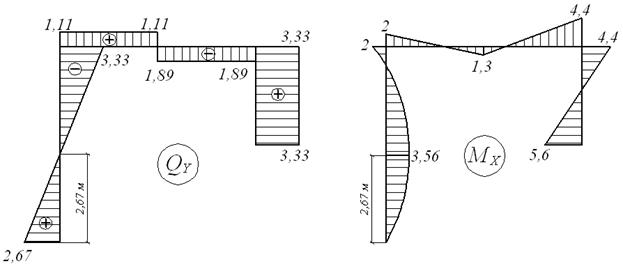
Будуємо епюри повздовжніх (N_z) і поперечних (Q_y) сил і згинальних моментів (М_х) для заданої системи з урахуванням обчислених реакцій зайвих зв'язків (мал.6.10,а-г).

Для виконання статичної перевірки необхідно вирізати жорсткі вузли рами 3 і 4 (мал.6.10,а) і переконатися в справедливості умов рівноваги для кожного з них.

Умови рівноваги для вузла 3 (мал.6.9,а):

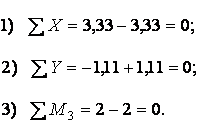
Умови рівноваги для вузла 4 (мал.6.9,б):

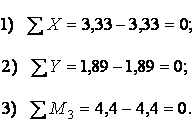
Таким чином, статична перевірка виконується.

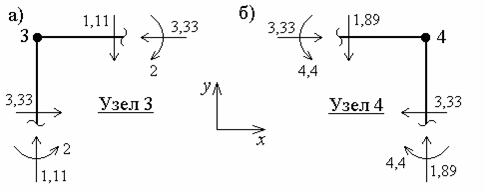
Рис.6.9. Статична перевірка (до прикладу 6.3)

Для виконання кінематичної перевірки перемножимо сумарну одиничну епюру 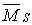(мал.6.8,е) і остаточну епюру згинальних моментів М_х (мал.6.10,г):

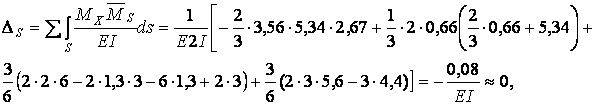
отже, усі перевірки методу сил виконуються, і розрахунок виконаний правильно.

а б

в г

Рис.6.10. Остаточні епюри (до прикладу 6.3)

Тепер розглянемо приклади, що ілюструють різні способи використання симетрії.

Приклад 6.4. Побудувати епюри N_z, Q_y і M_x для симетричної рами, завантаженою несиметричним зовнішнім навантаженням (мал.6.11,а).

Задана рама має два замкнутих безшарнірних контури, отже, її ступінь статичної невизначеності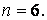

Записана формально, без використання симетрії, система канонічних рівнянь методу сил має вигляд

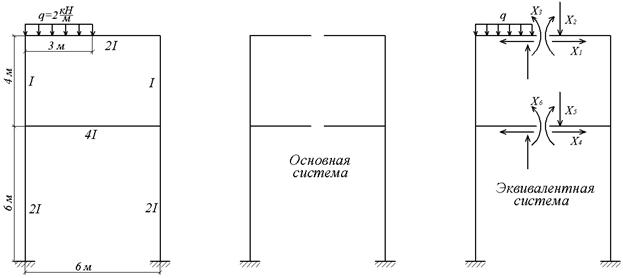
З багатьох можливих варіантів вибору основної системи найбільш доцільним, що максимально спрощує розрахунок, є варіант, представлений на мал.6.11,б, отриманий шляхом розрізування кожного з ригелів посередині прольоту. Тому що розріз стержня приводить до появи трьох невідомих факторів (двох сил і моменту), то еквівалентна система (мал.6.11,в) буде складатися з двох жорстко затиснених рам, одна з яких завантажена тільки невідомими реакціями, а інша — такими ж невідомими реакціями і зовнішнім навантаженням.

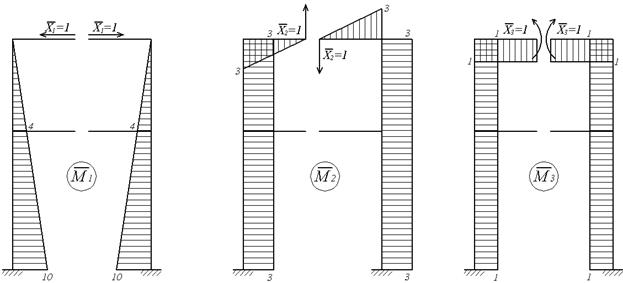
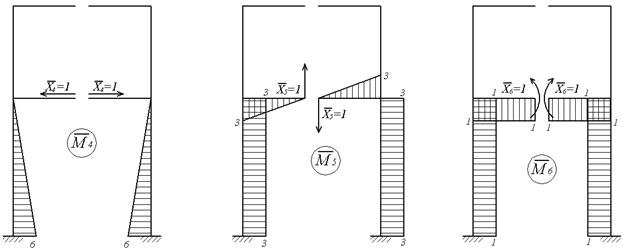
Зазначений вибір основної системи дозволяє не тільки одержати прості одиничні епюри (мал.6.11,г-і), але, що особливо важливо, при цьому цілий ряд побічних коефіцієнтів системи канонічних рівнянь звертається в нуль. Це ті коефіцієнти, що виходять шляхом перемножування симетричної і кососиметричної епюр:

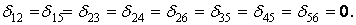
В силу теореми про взаємність переміщень число нульових коефіцієнтів подвоюється. У результаті формально записана система канонічних рівнянь розпадається на дві самостійні систем:

I)

II)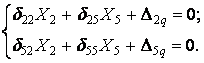

Обчислення коефіцієнтів цих систем рівнянь (з обов'язковим обліком співвідношення жорсткостей елементів) приводить до наступних результатів:

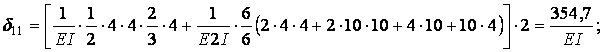
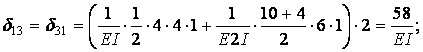
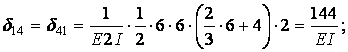
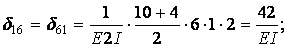
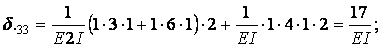
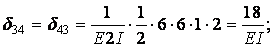
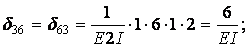
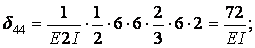
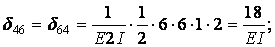
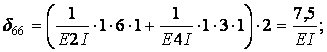
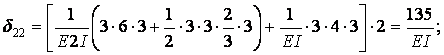
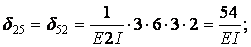
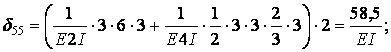
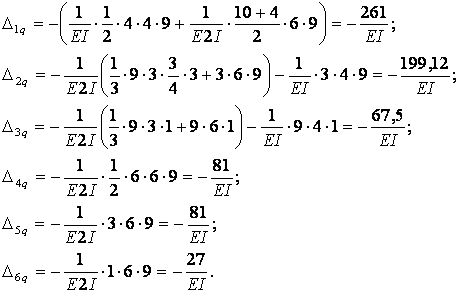
а	б	в
г	д	е
ж	з	і

Рис.6.11. Використання симетрії (до прикладу 6.4)

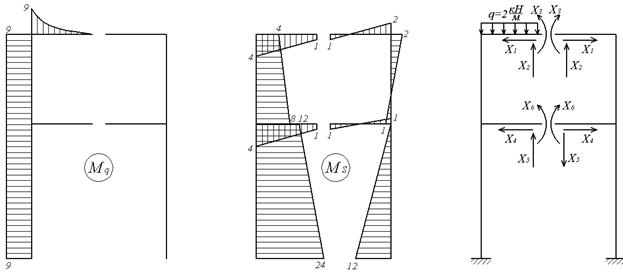
Для виконання перевірки обчислених переміщень будуємо сумарну одиничну епюру 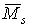від одночасної дії шести одиничних факторів (мал.6.12,б).

Обчислюємо коефіцієнти 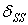і :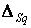

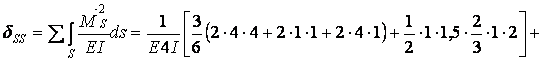
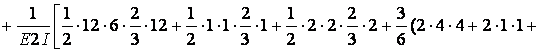
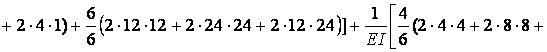
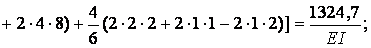
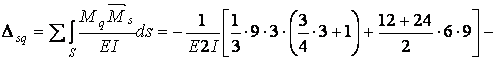
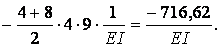
Виконуємо перевірку:

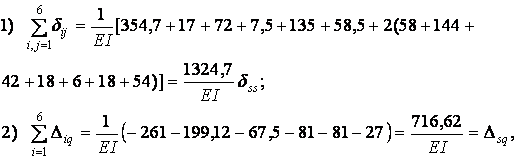
отже, коефіцієнти і вільні члени систем канонічних рівнянь обчислені правильно.

а	б	в
г	д	е

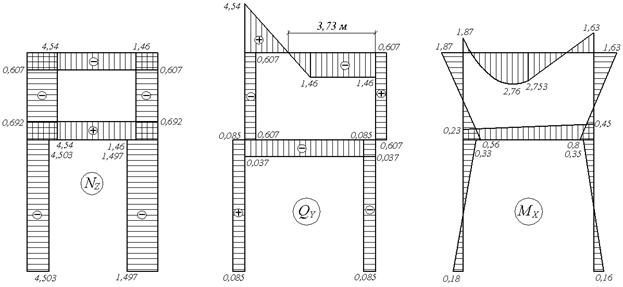
Рис.6.12. Остаточні епюри (до прикладу 6.4)

Підставляючи обчислені значення переміщень, одержимо системи канонічних рівнянь I і II у вигляді:

I.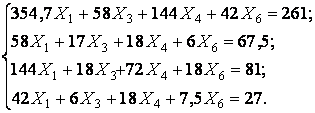

II.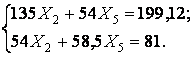

Розв’язання систем I і II дає значення реакцій зайвих зв'язків:

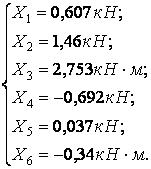
Остаточні епюри N_z, Q_y, M_x, побудовані від одночасної дії обчислених реакцій і зовнішнього навантаження q (мал.6.12,в) показані на мал.6.12,м,д,е.

НАЗАД ДО ЗМІСТУ ДАЛІ

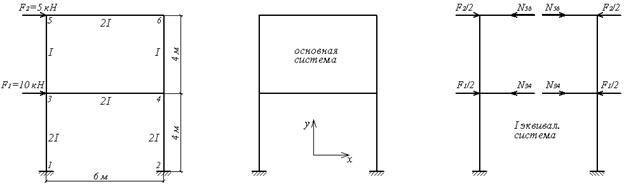
Приклад 6.5. Побудувати епюри N_z, Q_y, M_x у симетричній рамі (мал.6.13,а).

Рама має два замкнутих безшарнірних контури, тому вона шість разів статично невизначена. При звичайному підході в цьому випадку було б необхідно вирішити систему шести лінійних рівнянь, тобто розрахунок був би досить трудомістким. Використання симетрії, як це буде показано нижче, дозволить звести задачу до розв’язання тільки лише двох лінійних рівнянь.

Виберемо основну систему, розрізаючи кожний з ригелів посередині прольоту (мал.6.13,б). Але, на відміну від попереднього прикладу, сформуємо дві еквівалентні системи, одну з яких завантажимо симетричними складовими зовнішнього навантаження (мал.6.13,в), а іншу — зворотно симетричними складовими (мал.6.13,г). Легко переконатися в тому, що сума зовнішніх навантажень, прикладених до обох еквівалентних систем, дорівнює зовнішньому навантаженню, прикладеному до заданої рами.

При дії симетричних самоурівноважених сил 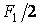і 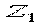(мал.6.13,в), прикладених у вузлах, в елементах рами відсутні згинальні моменти і поперечні сили, а повздовжні сили виникають тільки в ригелях і обчислюються безпосередньо з умов рівноваги вузлів 3 і 5, або, що те ж саме, 4 і 6:

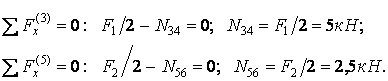
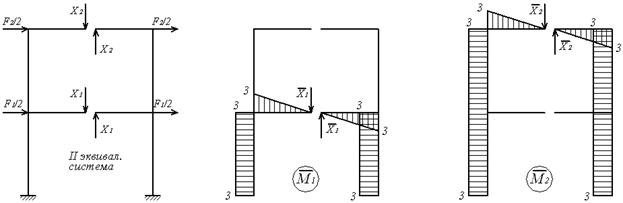
При дії зворотньосиметричних сил 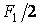і 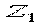(мал.6.13,г) у розрізах, зроблених по осі симетрії рами, виникають зворотньосиметричні невідомі поперечні сили Х₁, Х₂, а повздовжні сили і згинальні моменти звертаються в нуль як симетричні зусилля при зворотньосиметричному навантажені.

Таким чином, для розрахунку рами потрібно скласти тільки два канонічних рівняння методу сил:

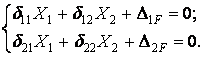
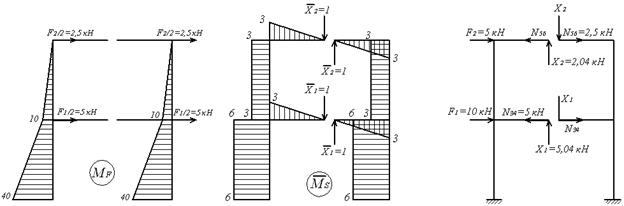
Одиничні і вантажна епюра згинальних моментів показані на мал.6.13,д,е,ж. Обчислимо коефіцієнти канонічних рівнянь шляхом перемноження відповідний епюр за правилом Верещагіна:

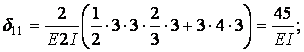
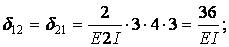
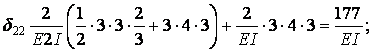
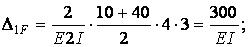
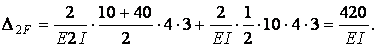
Одиничні і вантажна епюра згинальних моментів показані на мал.6.13,д,е,ж.

а	б	в
г	д	е
ж	з	і
к	л	м

Рис.6.13. До прикладу 6.5

Для перевірки обчислених переміщень використовуємо сумарну одиничну епюру згинальних моментів 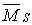(мал.6.13,з).

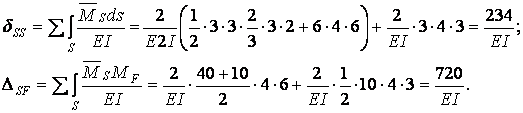
Перевірка:

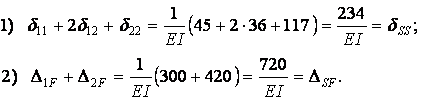
Після підстановки знайдених значень коефіцієнтів при невідомих і вільних членів у канонічні рівняння і множення останніх на EI одержимо

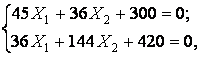
звідси

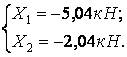
Таким чином, у результаті розкриття статичної невизначеності вихідна, шість разів статично невизначена система приведена до статично визначної системи (мал.6.13,і), завантаженої зовнішнім навантаженням F₁ і F₂, повздовжніми зусиллями N₃₄ і N₅₆, а також обчисленими реакціями X₁ і X₂.

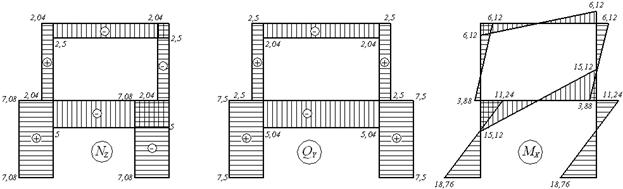
Епюри повздовжніх, поперечних сил і згинальних моментів для заданої рами показані на мал.6.13,к,л,м.

Для виконання універсальної кінематичної перевірки епюри М_х використовуємо сумарну одиничну епюрові :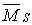

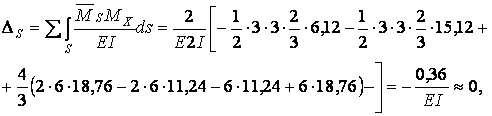
отже, задача вирішена правильно.

Приклад 6.6. Побудувати епюри згинальних моментів для статично невизначеної рами (мал.6.14,а), використовуючи спосіб введення жорстких консолей.

Цей спосіб використовується для ортогоналізації епюр (тобто для одержання нульових переміщень — коефіцієнтів канонічних рівнянь) у межах кожного замкнутого або відкритого з затисненими кінцями симетричного контуру. Для ортогоналізації епюр за допомогою жорстких консолей відповідні невідомі переносяться в деяку точку, названу пружним центром. Положення цієї точки визначається як положення центра тяжіння умовного тонкостінного перетину з товщиною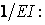

Задана рама має ступінь статичної невизначеності:

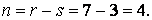
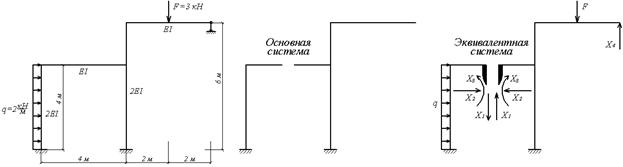
Для вибору основної системи (мал.6.14,б) використовуємо ту обставину, що лівий (П-подібний) контур рами симетричний. Розріжемо його по осі симетрії, що буде еквівалентно видаленню трьох зв'язків і появі трьох невідомих реакцій. Четвертий зв'язок усунемо шляхом видалення шарнірно-рухомої опори. Введення в місці розрізу жорстких консолей із прикладеними на їхніх кінцях реакціями Х₁, Х₂, Х₃ разом з реакцією Х₄ і зовнішніми навантаженнями приводить до еквівалентної системи (мал.6.14,в).

Визначимо положення пружного центру, тобто фактично довжину жорстких консолей (мал.6.14,г), обчислюючи координати центра тяжіння умовного тонкостінного П-подібного перетину:

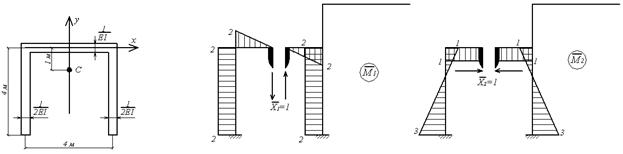
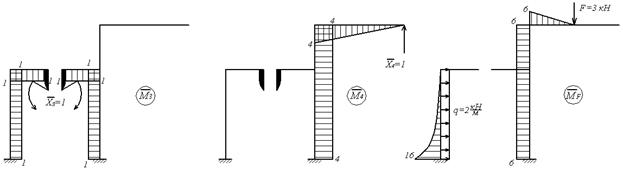
Одиничні епюри згинальних моментів показані на мал.6.14,д,е,ж,з, а епюра моментів від зовнішніх навантажень – на мал.6.14,і.

Враховуючи, що результат перемноження симетричної епюри на кососиметричну дорівнює нулеві, систему канонічних рівнянь методу сил розглянутої рами запишемо в вигляді

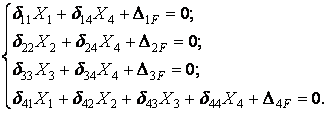
Обчислимо коефіцієнти рівнянь, використовуючи, як звичайно, спосіб Верещагіна:

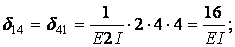
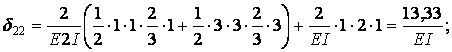
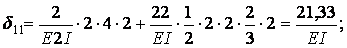
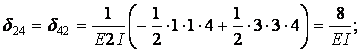
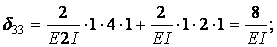
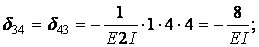
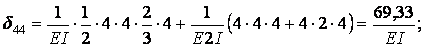
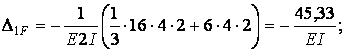
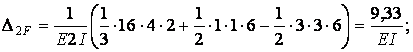
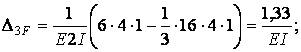
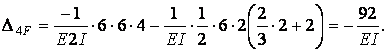
а	б	в
г	д	е
ж	з	і

Рис.6.14. Спосіб введення жорстких консолей (до прикладу 6.6)

Для перевірки правильності обчислення коефіцієнтів і вільних членів канонічних рівнянь побудуємо сумарну одиничну епюру згинальних моментів 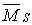(мал.6.15,а) і визначимо коефіцієнти 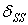і .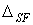

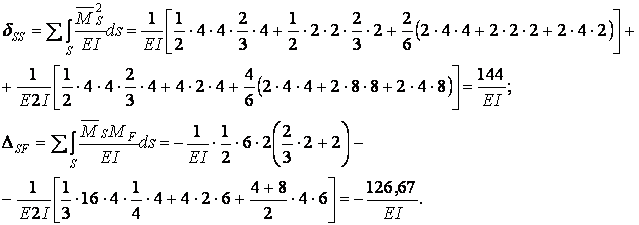
а	б

Рис.6.15. Сумарна одинична і кінцева епюри (до прикладу 6.6)

Перевірка:

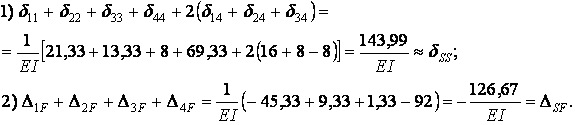
Отже, коефіцієнти і вільні члени канонічних рівнянь обчислені правильно. Розв’язок системи канонічних рівнянь дає наступні значення невідомих:

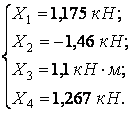
Остаточна епюра моментів для заданої рами показана на мал.6.15,б.

Можна самостійно переконатися в правильності побудови епюри, перемноживши її із сумарною одиничною епюрю 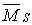(результат, як відомо, повинний дорівнювати нулеві).