Замена переменной в определенном интеграле

Теорема 6.Если выполнены условия:

1) функция f(x) непрерывна на отрезке [a, b];

2) отрезок [a, b] является множеством значений функции x = φ(t), определен­ной на отрезке α ≤ t ≤ β и имеющей на нем непрерывную производную;

3) φ(α) = a и φ(β) = b, то справедлива формула

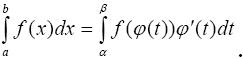
Замечание 1. При вычислении определенного интеграла методом замены переменной не нужно возвращаться к старой переменной.

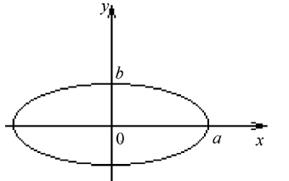П р и м е р. Вычислить площадь эллипса

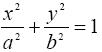(рис.).

Решение. Из уравнения эллипса находим

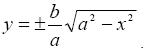
Вычислим площадь ограниченную верхней половиной эллипса

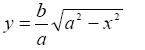
и осью OX (−a ≤ x ≤ a).

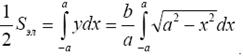
Сделаем подстановку x = sin t. Такая замена переменной удовлетворяет всем условиям теоремы 6. Действительно, x = sin t дифференцируема. При x = − a ⇒ − a = a sin t ⇒ sin t = − 1 ⇒ . При x = a ⇒ a sin t = a, .

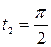На 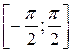x _t′= аcos x непрерывна и при изменении t от до 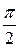функция a sin t возрастает от – a до a. Итак,

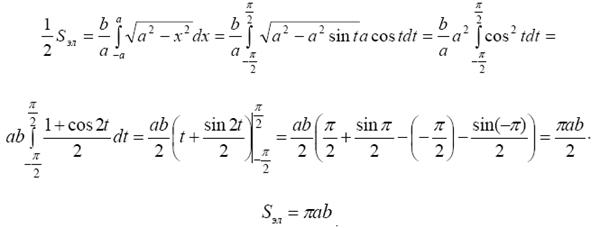
Замечание 2. При замене переменной необходимо следить за выполне­нием всех условий теоремы 6, иначе замена может привести к неверному результату.