Вычисление объемов.
2.1. Вычисление объема тела по известным площадям параллельных сечений. Если известны площади сечений тела плоскостями, перпендикулярными оси OX, т. е., зная х, мы можем вычислить площадь сечения S = S (x). Тогда объем тела 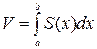 в предположении, что S(x) − интегрируемая функция.
в предположении, что S(x) − интегрируемая функция.
2.2. Вычисление объема тела вращения:
а) если тело образовано вращением криволинейной трапеции, ограниченной кривой y = f(x), осью OX и двумя прямыми x = a и x = b(a < b) вокруг оси OX, то объем тела
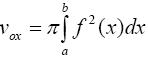
б) если тело образовано вращением фигуры, ограниченной кривой
x = j(y) , прямыми y=c, y=d (c<d) и осью OY, вокруг оси OY, то его объем
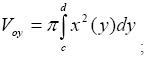
в) если тело образовано вращением вокруг оси OY фигуры, ограниченной линией y = f (x), прямыми x = a, x = b (0 ≤ a ≤ b) и осью OX, то его объем можно вычислить по формуле
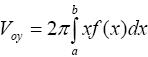
П р и м е р. Вычислить объем тела, образованного вращением фигуры, ограниченной графиками функций y = 2x − x2 и y = 2 − x вокруг оси OX.
Решение. Найдем точки пересечения параболы y = 2x − x2 и прямой y = 2 − x . Решим систему:
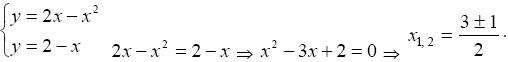
Получим две точки пересечения: х1 = 1, у1 = 1; х2 = 2, у2 = 0. Сделаем чертеж (рис. 19).
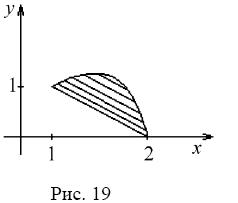
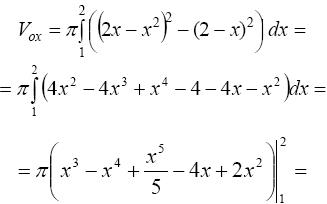
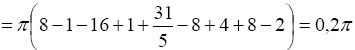
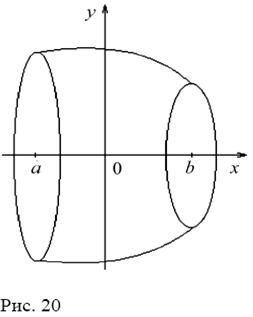
П р и м е р. Вычислить объем тела, ограниченного поверхностями:
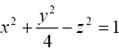 ; z = 0; z = 3.
; z = 0; z = 3.
Решение.
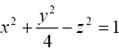 − однополостной гиперболоид. При пересечении его плоскостями z = h в сечении получаем эллипсы
− однополостной гиперболоид. При пересечении его плоскостями z = h в сечении получаем эллипсы
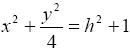
(рис. 20) с полуосями
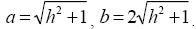
Как известно, площадь эллипса S =πab, тогда S(h) = 2π(h2 +1) 0 ≤ h ≤ 3
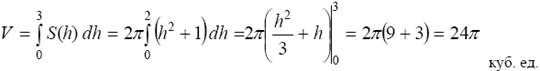
Дата добавления: 2015-01-24; просмотров: 4505;
