Признаки сходимости несобственных интегралов

1. Признак сравнения. Если при x ≥ a выполнены неравенства

0 ≤ j (x) ≤ f (x)

то:

а) из сходимости 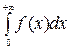следует сходимость ;

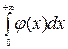б) из расходимости 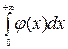следует расходимость .

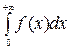2. Предельный признак сравнения. Если f(x) и φ(x) непрерывны и знако­постоянны на [a, ∞] и

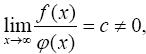
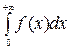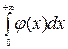то оба интеграла и сходятся либо расходятся одновре­менно.

3. Абсолютная сходимость. Если несобственный интеграл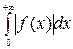

сходится, то сходится и интеграл 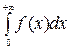и последний в этом случае называется абсолютно сходящимся.

Аналогичные признаки имеют место для несобственных интегралов от неограниченных функций.

П р и м е р. Исследовать на сходимость интеграл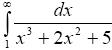

Решение. 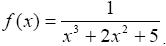Рассмотрим функцию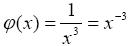

Интеграл 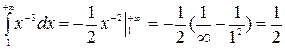сходится.

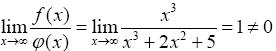
В силу предельного признака сравнения 2 исходный интеграл сходится.