Абсолютная сходимость несобственных интегралов 1-го рода.

Определение 15.2. Несобственный интеграл 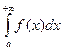называют абсолютно сходящимся, если сходится интеграл 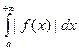. Функция f(x) называется при этом абсолютно интегрируемойна [a,∞).

Признак абсолютной сходимости несобственного интеграла (критерий Коши) – без доказательства.

Для того, чтобы 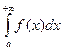абсолютно сходился, необходимо и достаточно, чтобы для любого ε > 0 существовало такое η, что при η΄ > η, η΄΄ > η .

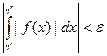Теорема 15.2. Если интеграл 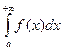абсолютно сходится, то он сходится и в обычном смысле.

Доказательство.

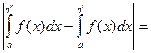
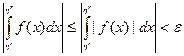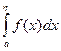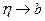Согласно критерию Коши . Следовательно, существует конечный предел при , то есть

рассматриваемый интеграл сходится.