Несобственные интегралы с бесконечными пределами (несобственные

интегралы 1-го рода)

Пусть функция f(x) определена и непрерывна при х ≥ а. Тогда интеграл 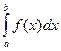имеет смысл при любом b > a и является непрерывной функцией аргумента b.

Определение 15.1. Если существует конечный предел

, (15.1)

то его называют несобственным интегралом 1-го рода от функции f(x) на интервале 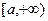и обозначают 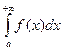. Таким образом, по определению

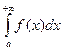= . (15.2)

При этом говорят, что несобственный интеграл существует или сходится. Если же не существует конечного предела (15.1), несобственный интеграл не существует или расходится.

y Повторим, что геометрической интерпрета-

y=f(x) цией несобственного интеграла 1-го рода

является площадь неограниченной области,

расположенной между графиком функции

y=f(x) , прямой х = а и осью Ох.

a b

Замечание. Аналогичным образом можно определить и несобственные интегралы 1-го рода для других бесконечных интервалов:

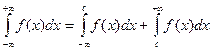(15.3)

В частности, последний интеграл существует только в том случае, если сходятся оба интеграла, стоящие в правой части равенства.

Часто достаточно бывает только установить сходимость или расходимость несобственного интеграла и оценить его значение.

Лемма.

Если 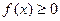на интервале [a, +∞), то для сходимости интеграла 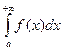необходимо и достаточно, чтобы множество всех интегралов 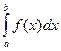(b > a) было ограничено сверху, то есть чтобы существовала такая постоянная c > 0, чтобы 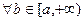выполнялось неравенство 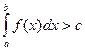. (15.4)

Доказательство.

Рассмотрим функцию 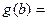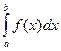и покажем, что в условиях леммы она монотонно возрастает на [a, +∞). Действительно, при = +

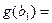
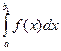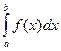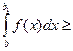
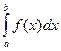+ =g(b), так как при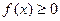 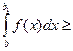0. Следовательно, функция g(b) монотонно возрастает и ограничена сверху, поэтому она имеет конечный предел при 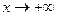, что по определению означает существование интеграла .

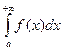Теорема 15.1 (признак сравнения). Пусть при 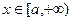. Тогда:

1) если интеграл 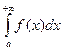сходится, то сходится и интеграл ;

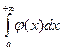2) если интеграл 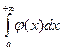расходится, то расходится и интеграл .

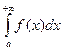Доказательство.

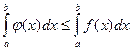
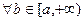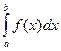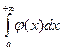Из условия теоремы следует, что . Поэтому, если интегралы ограничены сверху (по лемме), то сверху ограничены и интегралы , следовательно, сходится (по той же лемме). Если же интеграл 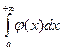расходится, то, если бы интеграл 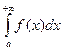сходился, то по ранее доказанному 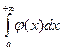должен был бы сходиться, что противоречит сделанному предположению. Значит, в этом случае 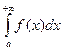расходится. Теорема полностью доказана.

Следствие.

Пусть 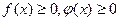на [a,∞), 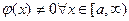и существует конечный или бесконечный предел , то:

а) если интеграл 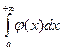сходится и 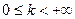, то сходится и интеграл ;

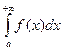б) если интеграл 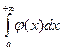расходится и 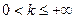, то интеграл 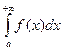тоже расходится.

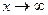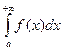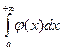В частности, если k = 1, то есть функции f(x) и φ(х) эквивалентны при , то интегралы и сходятся и расходятся одновременно.

При применении признака сравнения удобно сравнивать подынтегральную функцию с функцией 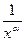, α > 0, для которой сходимость или расходимость соответствующего несобственного интеграла легко установить непосредственно. Пусть 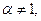тогда

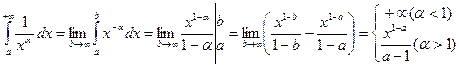. При α = 1

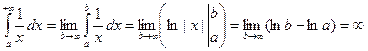. Следовательно, 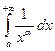сходится при α > 1 и расходится при α ≤ 1.

Пример.

Исследуем на сходимость 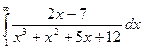. При 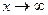подынтегральная функция эквивалентна 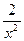. Таким образом, α = 2 > 1, и данный интеграл сходится.