Свойства определенного интеграла.
Сформулируем понятия верхней и нижней интегральных сумм. Пусть тi – наименьшее значение функции f (x) на отрезке Δxi , а Mi – ее наибольшее значение на этом отрезке.
Определение 11.2. Сумма sn = 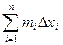 называется нижней интегральной суммой функции f (x) на [a,b], а Sn =
называется нижней интегральной суммой функции f (x) на [a,b], а Sn = 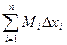 - верхней интегральной суммой.
- верхней интегральной суммой.
Свойства интегральных сумм.
- Так как на любом отрезке разбиения mi ≤ Mi , то si ≤ Si .
2. Если т – наименьшее значение f(x) на [a,b], а М – ее наибольшее значение на [a,b], то 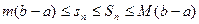 .
.
3. При добавлении к выбранному разбиению новых точек sn может только возрастать, а Sn – только уменьшаться.
Доказательство.
Пусть отрезок [xk-1 ,xk] разбит на р отрезков. Обозначим нижнюю и верхнюю интегральные суммы на этих отрезках как sp и Sp. Но для отрезка [xk-1 ,xk] наименьшим значением функции является тк, а наибольшим – Мк. Следовательно, по свойству 2 sp ≥ mk Δxk – соответствующему слагаемому общей интегральной суммы s , а Sk≤ Mk Δxk – слагаемому верхней интегральной суммы. Таким образом, каждое слагаемое s может только увеличиваться при добавлении новых точек, а каждое слагаемое S – только уменьшаться, что и доказывает сформулированное утверждение.
- Существуют
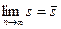 и
и  .
.
Доказательство.
Из свойств 2 и 3 следует, что s ограничена ( 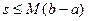 ) и монотонно возрастает. Следовательно, она имеет предел. Подобное же рассуждение справедливо для S.
) и монотонно возрастает. Следовательно, она имеет предел. Подобное же рассуждение справедливо для S.
- Если f (x) непрерывна на [a,b], то
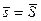 .
.
Доказательство.
Назовем колебаниемфункции f (x) на отрезке Δхк разность ωk = Mk – mk. Тогда в силу непрерывности f (x) 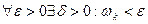 при
при 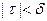 . Следовательно,
. Следовательно, 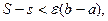 то есть
то есть 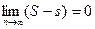 , что и требовалось доказать.
, что и требовалось доказать.
Замечание. Так как s и S можно считать частными случаями интегральных сумм функции f (x), то 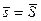 =
= 
- Для любых двух разбиений данного отрезка τ1 и τ2
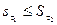 .
.
Для доказательства этого утверждения достаточно рассмотреть разбиение, включающее все точки разбиений τ1 и τ2 , и воспользоваться свойствами 1 и 3.
Перечислим основные свойства определенного интеграла.
- Постоянный множитель можно выносить за знак интеграла:
 .
.
Доказательство.
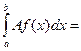
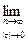
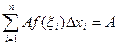
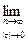
 =
= 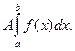
2. 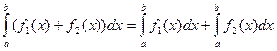 .
.
Доказательство.
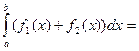
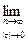
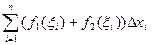 =
= 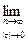 (
( 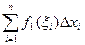 +
+ 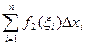 ) =
) =
= 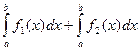 .
.
3.Если на отрезке [a,b] (a<b) f (x) ≤ g (x), то 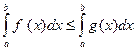 .
.
Доказательство.
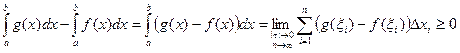 , так как
, так как 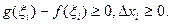 Отсюда следует, что
Отсюда следует, что 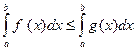 .
.


 у А2 В2 Геометрическая интерпретация:
у А2 В2 Геометрическая интерпретация:
 площадь криволинейной трапеции аА1В1b не
площадь криволинейной трапеции аА1В1b не
 больше площади аА2В2b.
больше площади аА2В2b.
A1 B1
 a b
a b
4. Если т и М – наименьшее и наибольшее значения функции f(x) на отрезке [a,b], 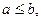 то
то 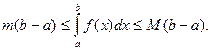
Доказательство.

 Так как
Так как 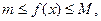 по свойству 3
по свойству 3 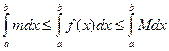 . Но
. Но 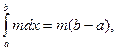
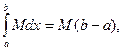 следовательно,
следовательно, 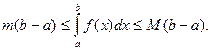



 у А2 В2 Геометрическая интерпретация:
у А2 В2 Геометрическая интерпретация:
площадь криволинейной трапеции содержится
М между площадями прямоугольников aA1B1b и
aA2B2b.

 А1 т В1
А1 т В1
а b
5 (Теорема о среднем). Если функция f(x) непрерывна на отрезке [a,b], то на этом отрезке найдется такая точка ξ, что 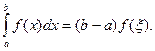
Доказательство.
Пусть 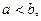 т и М – наименьшее и наибольшее значения функции f(x) на [a,b]. Тогда по свойству 4
т и М – наименьшее и наибольшее значения функции f(x) на [a,b]. Тогда по свойству 4 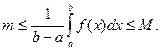 Тогда
Тогда 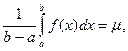
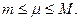 Так как f(x) непрерывна на [a,b], она принимает на нем все промежуточные значения между т и М, то есть существует
Так как f(x) непрерывна на [a,b], она принимает на нем все промежуточные значения между т и М, то есть существует 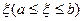 такое, что
такое, что 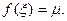 Тогда
Тогда 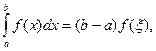 что и требовалось доказать.
что и требовалось доказать.
- Для любых трех чисел a,b,c справедливо равенство
 ,
,
если все эти интегралы существуют.
Доказательство.
Пусть a < c < b. Составим интегральную сумму так, чтобы точка с была точкой деления. Тогда 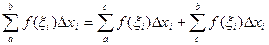 . Переходя к пределу при
. Переходя к пределу при 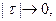 получим доказательство свойства 6.
получим доказательство свойства 6.
Если a < b < c, то по только что доказанному 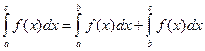 , или
, или 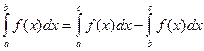 . Но
. Но 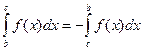 , поэтому
, поэтому  . Аналогично доказывается это свойство и при любом другом расположении точек a, b и с.
. Аналогично доказывается это свойство и при любом другом расположении точек a, b и с.
Лекция 12.
Интегрируемость непрерывных, кусочно-непрерывных и монотонных ограниченных функций. Производная интеграла по переменному верхнему пределу. Формула Ньютона – Лейбница.
Теорема 12.1. Функция, непрерывная на отрезке, интегрируема на нем.
Доказательство.
Если функция f(x) непрерывна на отрезке [a,b], то она, во-первых, ограничена на нем, а во-вторых, равномерно непрерывна, то есть 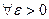
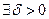 такое, что
такое, что 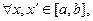
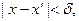
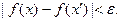 Тогда для разбиения, в котором
Тогда для разбиения, в котором 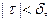 колебание
колебание 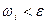 , следовательно,
, следовательно, 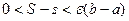 , и по свойству 5 верхних и нижних интегральных сумм получим, что существует
, и по свойству 5 верхних и нижних интегральных сумм получим, что существует 
Теорема 12.2. Функция, монотонная на отрезке, интегрируема на нем.
Доказательство.
Пусть f(x) возрастает на [a,b]. Тогда 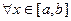
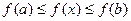 , то есть f(x) ограничена на [a,b]. Кроме того, для любого интервала [xi-1, xi]
, то есть f(x) ограничена на [a,b]. Кроме того, для любого интервала [xi-1, xi] 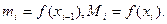 Следовательно,
Следовательно, 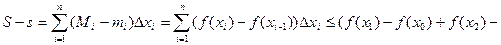
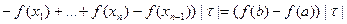 . Поэтому
. Поэтому  , следовательно, f(x) интегрируема на [a,b].
, следовательно, f(x) интегрируема на [a,b].
Замечание. В теореме 12.2 не требовалась непрерывность функции. Монотонная функция может быть и разрывной, при этом она является интегрируемой по теореме 12.2.
Теорема 12.3. Если f(x) – непрерывная функция и 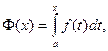 то
то 
(Производная от определенного интеграла по верхнему пределу равна подынтегральной функции, в которую вместо переменной интегрирования подставлено значение верхнего предела).
Доказательство.
Пусть Δх – приращение аргумента х. Тогда по свойству 6 определенного интеграла
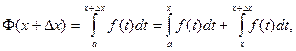
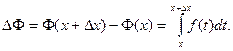
По теореме о среднем (свойство 5) 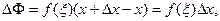 где
где  . Поэтому
. Поэтому  Следовательно,
Следовательно,  Но при
Но при 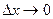
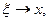 и вследствие непрерывности функции f(x)
и вследствие непрерывности функции f(x) 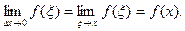 Таким образом,
Таким образом,  Теорема доказана.
Теорема доказана.
Замечание. Из теоремы 12.3 следует, что всякая непрерывная функция имеет первообразную, так как по теореме 12.1 она интегрируема, а по теореме 12.3 ее первообразной является 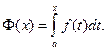
Теорема 12.4. Если F(x) является первообразной непрерывной функции f(x), то справедлива формула
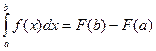 , (12.1)
, (12.1)
называемая формулой Ньютона – Лейбница.
Доказательство.
По теореме 12.3 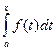 - первообразная функции f(x), поэтому F(x) и
- первообразная функции f(x), поэтому F(x) и 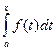 отличаются на постоянное слагаемое С. Следовательно,
отличаются на постоянное слагаемое С. Следовательно, 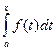 = F(x) + C. (12.2)
= F(x) + C. (12.2)
Пусть х=а, тогда из (12.2) получим 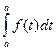 = F(a) + C, то есть F(a) + C = 0, откуда
= F(a) + C, то есть F(a) + C = 0, откуда
C = - F(a). Тогда 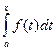 = F(x) – F(a). Принимая в этом равенстве x=b, получим формулу Ньютона – Лейбница:
= F(x) – F(a). Принимая в этом равенстве x=b, получим формулу Ньютона – Лейбница: 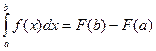 .
.
Замечание. Обычно вводится обозначение 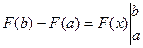 , и формула (12.1) записывается так:
, и формула (12.1) записывается так:  .
.
Примеры.
1. 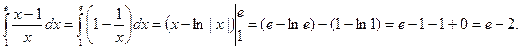
2. 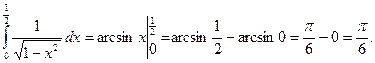
Лекция 13.
Замена переменной и интегрирование по частям в определенном интеграле. Применение определенного интеграла к вычислению площадей плоских фигур.
Теорема 13.1. Если:
1) функция f(x) непрерывна на отрезке [a,b],
2) функция φ(t) непрерывна и имеет непрерывную производную φ΄(t) на отрезке [α,β], где a = φ(α), b = φ(β),
3) функция f (φ(t)) определена и непрерывна на отрезке [α,β],
то 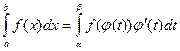 . (13.1)
. (13.1)
Доказательство.
Если F(x) – первообразная для f(x), то 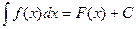 ,
,
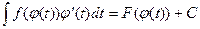 (см. теорему 6.2). Тогда, используя формулу Ньютона – Лейбница, получим:
(см. теорему 6.2). Тогда, используя формулу Ньютона – Лейбница, получим: 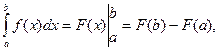
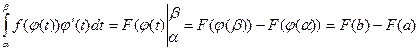 , откуда следует справедливость формулы (13.1).
, откуда следует справедливость формулы (13.1).
Замечание. В отличие от неопределенного интеграла, в определенном интеграле нет необходимости возвращаться к прежней переменной интегрирования, так как результатом вычисления будет число, не зависящее от выбора переменной.
Пример.
Вычислить интеграл 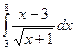 . Сделаем замену:
. Сделаем замену: 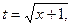 откуда
откуда 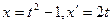 . При этом
. При этом 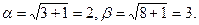 Тогда
Тогда 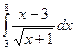 =
= 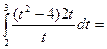
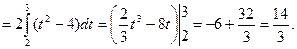
Теорема 13.2. Если функции u(x) и v(x) непрерывны вместе со своими производными на отрезке [a,b], то
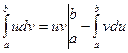 .(13.2)
.(13.2)
(Формула (13.2) называется формулой интегрирования по частямдля определенного интеграла).
Доказательство.
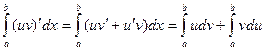 . Все интегралы в этом равенстве существуют, так как подынтегральные функции непрерывны. При этом
. Все интегралы в этом равенстве существуют, так как подынтегральные функции непрерывны. При этом 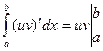 , поэтому
, поэтому  , откуда следует (13.2).
, откуда следует (13.2).
Примеры.
- Вычислить интеграл
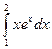 . Пусть u = x, dv = exdx. Тогда du = dx, v = ex. Применим формулу (13.2):
. Пусть u = x, dv = exdx. Тогда du = dx, v = ex. Применим формулу (13.2): 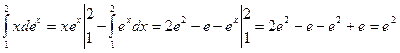 .
. -
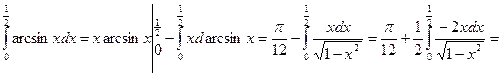
 . (При интегрировании принималось u = x, v = arcsinx).
. (При интегрировании принималось u = x, v = arcsinx). - Вычислить
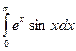 . Пусть u = ex, dv = sinxdx. Тогда du = exdx, v = -cosx. Следовательно,
. Пусть u = ex, dv = sinxdx. Тогда du = exdx, v = -cosx. Следовательно, 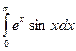 =
= 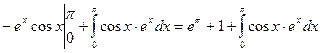 . Применим к интегралу в правой части полученного равенства еще раз формулу интегрирования по частям, положив u = ex, dv = cosxdx:
. Применим к интегралу в правой части полученного равенства еще раз формулу интегрирования по частям, положив u = ex, dv = cosxdx: 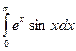 =
= 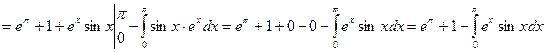 . Поскольку при этом в правой части равенства стоит такой же интеграл, как в левой, его значение можно найти из уравнения: 2
. Поскольку при этом в правой части равенства стоит такой же интеграл, как в левой, его значение можно найти из уравнения: 2 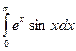 = eπ + 1 , то есть
= eπ + 1 , то есть
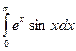 =
= 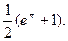
Дата добавления: 2015-03-19; просмотров: 1285;
