Площадь в полярных координатах. Длина дуги кривой и ее вычисление. Вычисление объемов тел.

Введем на плоскости криволинейную систему координат, называемую полярной. Она состоит из точки О (полюса) и выходящего из него луча (полярной оси).

у

М

ρ М

φ у=ρsinφ ρ

O

O x=ρcosφ x

Рис. 1 Рис. 2

Координатами точки М в этой системе (рис. 1) будут длина отрезка МО – полярный радиус ρ и угол φ между МО и полярной осью: М(ρ,φ). Отметим, что для всех точек плоскости, кроме полюса, ρ > 0, а полярный угол φ будем считать положительным при измерении его в направлении против часовой стрелки и отрицательным – при измерении в противоположном направлении.

Замечание. Если ограничить значения φ интервалом [0,π] или [-π, π], то каждой точке плоскости соответствует единственная пара координат (ρ,φ). В других случаях можно считать, что φ может принимать любые значения, то есть полярный угол определяется с точностью до слагаемого, кратного 2π.

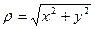Связь между полярными и декартовыми координатами точки М можно задать, если совместить начало декартовой системы координат с полюсом, а положительную полуось Ох – с полярной осью (рис. 2). Тогда x=ρcosφ, у=ρsinφ . Отсюда , tg 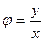. Выясним, как с помощью определенного интеграла вычислить площадь фигуры, границы которой заданы в полярных координатах.

а) Площадь криволинейного сектора. ρ=ρ₁(φ)

ρ=ρ(φ)

ρ=ρ₂(φ)

β α β α

О О

Рис. 3 Рис. 4

Найдем площадь фигуры, ограниченной частью графика функции ρ=ρ(φ) и отрезками лучей φ = α и φ = β. Для этого разобьем ее на п частей лучами φ = φ_i и найдем сумму площадей круговых секторов, радиусами которых служат где Как известно, площадь сектора вычисляется по формуле 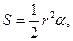где r – радиус сектора, а α – его центральный угол. Следовательно, для суммы площадей рассматриваемых секторов можно составить интегральную сумму 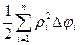, где 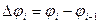. В пределе при 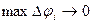получим, что площадь криволинейного сектора

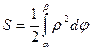. (14.1)

б) Площадь замкнутой области.

Если рассмотреть замкнутую область на плоскости, ограниченную кривыми, уравнения которых заданы в полярных координатах в виде 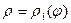и ( 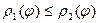), а полярный угол φ принимает для точек внутри области значения в пределах от α до β (рис. 4), то ее площадь можно вычислять как разность площадей криволинейных секторов, ограниченных кривым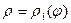и и , то есть

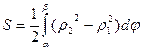. (14.2)

Пример.

Вычислим площадь области, заключенной между дугой окружности x² + y² = 1 и прямой x = 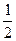при 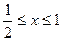. В точках пересечения прямой и окружности 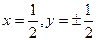, то есть полярный угол φ изменяется внутри области в пределах от 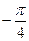до 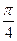. Уравнение окружности в полярных координатах имеет вид ρ = 1, уравнение прямой - 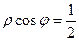, то есть . Следовательно, площадь рассматриваемой области можно найти по формуле (14.2):

.

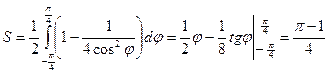1. Длина дуги кривой.

а) Длина дуги в декартовых координатах.

у y = f(x) Рассмотрим функцию y = f(x), непрерывную

Δу_i на отрезке [a,b] вместе со своей производной.

Δх_i Выберем разбиение τ отрезка [a,b] и будем

считать длиной дуги кривой, являющейся

графиком f(x), от х=а до x=b предел при |τ|→0

длины ломаной, проведенной через точки

графика с абсциссами х₀ , х₁ ,…, х_п (точками

а x_i-1 x_i b разбиения τ) при стремлении длины ее

наибольшего звена к нулю:

Рис. 5 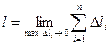. (14.3)

Убедимся, что при поставленных условиях этот предел существует. Пусть 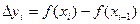. Тогда 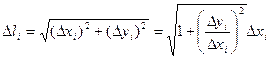(рис. 5).По формуле конечных приращений Лагранжа 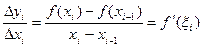, где x_i-1 < ξ_i < x_i . Поэтому 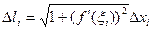, а длина ломаной . Из непрерывности f(x) и 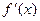следует и непрерывность функции , следовательно, существует и предел интегральной суммы, являющейся длиной ломаной, который равен

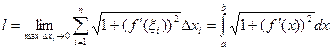. Таким образом, получена формула для вычисления длины дуги:

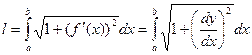. (14.4)

Пример.

Найти длину дуги кривой y = ln x от х = 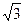до х = .

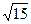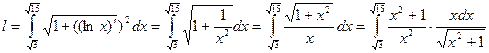. Сделаем замену: , тогда 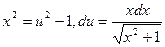, а пределами интегрирования для u будут u=2 (при х= 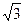) и и = 4 (при х = 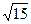). Получим: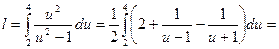

.

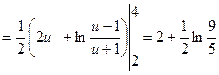б) Длина дуги кривой, заданной в параметрической форме.

Если уравнения кривой заданы в ви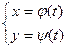де , где 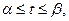а φ(t) и ψ(t) – непрерывные функции с непрерывными производными, причем φ΄(t) ≠ 0 на [α,β], то эти уравнения определяют непрерывную функцию y = f(x), имеющую непрерывную производную 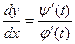. Если 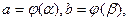то из (14.4) или

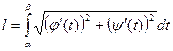. (14.5)

Замечание. Если пространственная линия задана параметрическими уравнениями

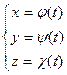, то при указанных ранее условиях 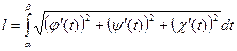.(14.6)

в) Длина дуги в полярных координатах.

Если уравнение кривой задано в полярных координатах в виде ρ = f(φ), то x = ρ cos φ = f(φ)cos φ, y = ρ sin φ = f(φ)sin φ – параметрические уравнения относительно параметра φ. Тогда для вычисления длины дуги можно использовать формулу (14.5), вычислив предварительно производные х и у по φ:

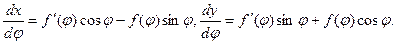Следовательно,

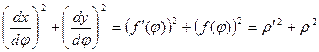, поэтому

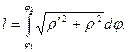(14.7)

Пример.

Найти длину дуги спирали Архимеда ρ = φ от φ = 0 до φ = 2π .

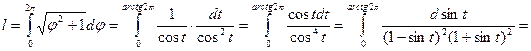
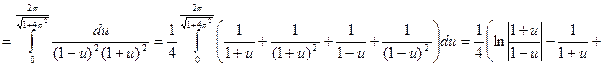
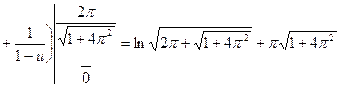(были применены замены φ = tg t и u = sint).

1. Вычисление объемов тел.

Пусть имеется некоторое тело, для которого известна площадь любого его сечения плоскостью, перпендикулярной оси Ох, являющаяся функцией от х: Q = Q(x). Определим объем рассматриваемого тела в предположении, что Q – непрерывная функция. Если значение х внутри тела меняется от а до b, то можно разбить тело на слои плоскостями х = х₀ = а, х = х₁, х = х₂,…, х = х_n = b. Затем выберем в каждом слое значение х = ξ_i , x_i-1 ≤ ξ_i ≤ x_i , и рассмотрим сумму объемов цилиндров с площадями оснований Q(ξ_i) и высотами Δx_i = x_i – x_i-1 . Эта сумма будет равна 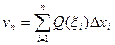. Получена интегральная сумма для непрерывной функции Q(x) на отрезке [a,b] , следовательно, для нее существует предел при | τ | → 0, который равен определенному интегралу

, (14.8)

называемому объемом данного тела.

Замечание. Если требуется определить объем так называемого тела вращения, то есть тела, образованного вращением вокруг оси Ох криволинейной трапеции, ограниченной частью графика функции y = f(x) от х = а до x = b и отрезками прямых х = а, х = b и у =0, то площадь сечения такого тела плоскостью x = constравна 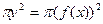, и формула (14.8) в этом случае имеет вид:

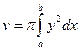
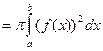. (14.9)

Пример.

Найдем объем эллипсоида вращения 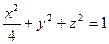. При x = const сечениями будут круги с радиусом 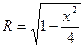и площадью 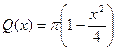. Применим формулу (14.8), учитывая, что х изменяется от –2 до 2:

v = .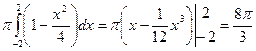

1. Площадь поверхности тела вращения.

Пусть требуется определить площадь поверхности, полученной вращением кривой y = f(x) вокруг оси Ох при . Выберем разбиение τ отрезка [a,b] и рассмотрим, как и при определении длины кривой, ломаную, проходящую через точки кривой с абсциссами x_i . Каждый отрезок такой ломаной при вращении опишет усеченный конус, площадь боковой поверхности которого равна 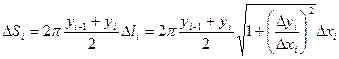. По формуле конечных приращений Лагранжа 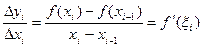, где . Поэтому 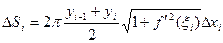. Следовательно, площадь всей поверхности, описанной ломаной при вращении, равна 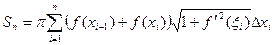. Назовем площадью поверхности вращения предел этой суммы при maxΔl_i →0 .

Заметим, что эта сумма не является интегральной суммой для функции 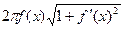, так как в каждом ее слагаемом фигурирует несколько точек данного отрезка разбиения. Однако можно доказать, что предел такой суммы равен пределу интегральной суммы для 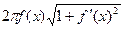, откуда получаем формулу для площади поверхности вращения:

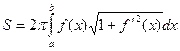. (14.10)

Пример.

Вычислим площадь поверхности, полученной вращением части кривой 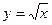от х = 0 до х=1. Используя формулу (14.10), получим: .

Лекция 15.

Несобственные интегралы с бесконечными пределами интегрирования. Теорема сравнения для интегралов от неотрицательных функций. Абсолютная и условная сходимость. Признак абсолютной сходимости. Несобственные интегралы от неограниченных функций, исследование их сходимости.

В предыдущих лекциях рассматривались определенные интегралы, соответствующие с геометрической точки зрения площадям замкнутых ограниченных областей (криволинейных трапеций). Расширим понятие определенного интеграла на случай неограниченной области. Такую область можно получить, либо приняв какой-либо из пределов интегрирования равным бесконечности, либо рассматривая график функции с бесконечными разрывами (то есть неограниченной). Рассмотрим отдельно каждый из указанных случаев.