Геометрические приложения определенного интеграла.

1. Вычисление площадей плоских фигур.

Вспомним, каким образом вводилось понятие определенного интеграла. С геометрической точки зрения интегральная сумма представляет собой (при f(x) ≥ 0) сумму площадей прямоугольников с основанием 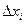и высотой 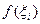. Переходя к пределу при |τ|→0, получаем, что 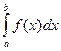при 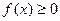представляет собой площадь так называемой криволинейной трапеции aА₁В₁b, то есть фигуры, ограниченной частью графика функции

у

у

y=f(x) y=f₂(x)

A₁ B₁

y=f₁(x)

a b х a b x

Рис. 1 Рис. 2

f(x) от х = а до x = b и отрезками прямых х = а, x = b и у = 0 (рис. 1):

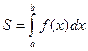. (13.3)

Если требуется найти площадь фигуры, ограниченной графиками двух функций: f₁(x) и f₂(x) (рис. 2), то ее можно рассматривать как разность площадей двух криволинейных трапеций: верхней границей первой из них служит график функции f₂(x), а второй – f₁(x). Таким образом, 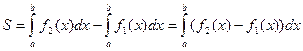. (13.4)

Замечание 1. Формула (13.4) справедлива, если графики функций f₁(x) и f₂(x) не пересекаются при a < x < b.

Замечание 2. Функции f₁(x) и f₂(x) могут при этом принимать на интервале [a,b] значения любого знака.

Пример.

Найти площадь фигуры, ограниченной графиками функций y = x² - 3x – 5 и y = x – 5.

Найдем абсциссы точек пересечения указанных графиков, то есть корни уравнения x² - 3x – 5 = x – 5. x² - 4x = 0, x₁ = a = 0, x₂ = b = 4. Таким образом, найдены пределы интегрирования. Так как на интервале [0,4] прямая y = x – 5 проходит выше параболы у = x² - 3x – 5, формула (13.4) примет вид: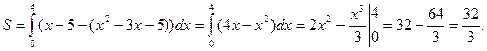

Лекция 14.