Геометрические параметры групповых объектов

Рассмотрим пример расчета геометрических характеристик изображения текста. Определим величину межстрочечного интервала и координаты центров строк. На рис. 2.22 представлено изображение текста, сигнал по столбцу с номером a - Y. Однако на приведенном сигнале даже человек вряд ли сможет распознать строки. Как уже указывалось, возможность распознавания можно улучшить, интегрируя участки изображения, в данном случае в направлении, перпендикулярном направлению анализа. Вычислим интегральный сигнал 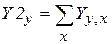, он также приведен на рис. 2.22 . На данном сигнале отчетливо видно хорошее различие заполненных черными точками текста участков.

Переходя в частотное пространство, определим величину интервала между строками. Уменьшим размер вектора до 64 (кратно 2 в степени n), и вычислим модуль F2 частотного спектра сигнала

,

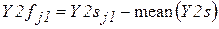где .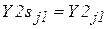

,

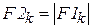где 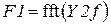– Фурье-образ Y2f, а k=0..c и – индекс последнего элемента вектора.

Вид спектра пространственных частот приведен на рис. 2.23.

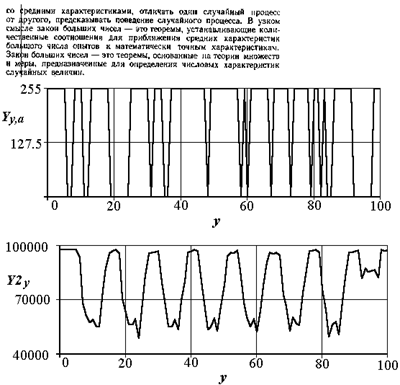
Рис. 2.22 . Бинаризованный текст, сечение по столбцу и интегральный сигнал

Интервал между строками в пикселях h равен:

,

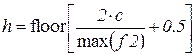где 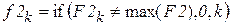– массив нулей с координатой максимума частотного спектра. В нашем случае h=13.

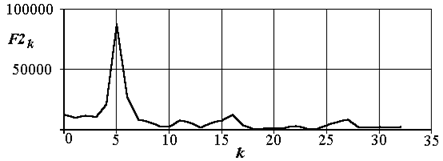
Рис. 2.23. Модуль частотного спектра интегрального сигнала

(постоянная составляющая отфильтрована)

Для определения координат центров строк введем фильтр F1 (рис. 2.24): 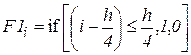, где .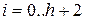

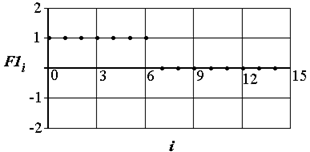
Рис. 2.24. Цифровой фильтр для определения координат центров строк

Вид выходного сигнала свертки сигнала Y2 c F1 показан на рис. 2.25.

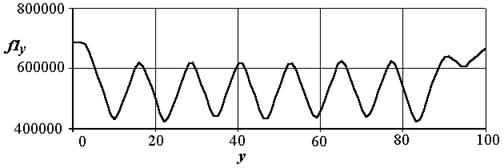
Рис. 2.25. Выходной сигнал после свертки Y2 c F1

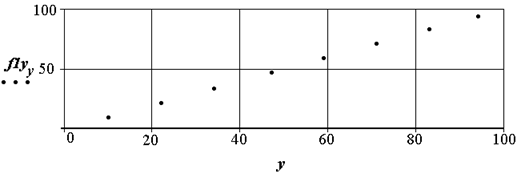
Рис. 2.26. Координаты центров строк

Составим вектор центров строк текста f1y, найдя координаты вершин через упрощенное выражение:

;

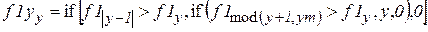где ym – число строк текста. Вид вектора представлен на рис. 2.26. Числа отличные от нуля являются координатами строк. Полученные числовые данные по положению строк текста приведены ниже.

{10, 22, 34, 47, 59, 71, 83, 94}