Общие сведения. Возможности цветового различия тесно связаны с понятием спектра длин волн оптического излучения, как информационного параметра сигнала с элемента изображения

Возможности цветового различия тесно связаны с понятием спектра длин волн оптического излучения, как информационного параметра сигнала с элемента изображения. В целом ряде случаев этот параметр избыточен. Более приемлемо характеризовать объект совокупностью меньшего количества компонент

,

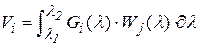где i – номер компонента (от 1 до N),

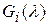– спектральная чувствительность i – канала,

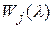- спектральная плотность потока от j – го объекта попавшая в i – канал,

λ – длина волны оптического излучения,

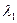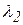... – рабочий диапазон длин волн.

Часто при распознавании можно отказаться от использования информации об общем уровне освещенности, перейдя в пространство цветов. Это понижает размерность исходного пространства на единицу и облегчает процедуру распознавания. Сформируем нормированные, не зависящие от общего уровня сигнала цветовые составляющие:

.

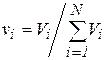Величина N определяет размерность цветового пространства 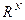до нормировки или 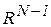после нормировки ( 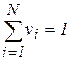). Часто говорят о N – компонентном цветовом пространстве. Очень распространена трехцветная модель RGB в видимом диапазоне длин волн оптического излучения. Она отображает чувствительность рецепторов глаза человека. Для данного диапазона создана недорогая аппаратура считывания и генерации изображений, разработаны стандарты описаний файлов и имеется множество графических программных продуктов для работы с ними. Как правило, информационное наполнение изображений, полученных не в RGB пространстве, переносят в него для более естественного анализа.

Процедура отображения изображений в пространство RGB содержит однозначную операцию отображения пикселя, которая состоит в последовательности следующих шагов:

· формируются матрицы R, G, и B в двухмерном геометрическом пространстве;

· формируется новая матрица с числом столбцов равным числу уровней квантования первой цветовой составляющей и числом строк равным числу уровней квантования второй цветовой составляющей пикселя;

· матрица заполняется тегом отсутствия запроса ячейки, например, - 256, данное число выбирается вне зоны существования уровней квантования третьей цветовой составляющей пикселя;

· в матрицу по координатам описания первой и второй цветовых составляющих записывается значение третьей цветовой составляющей пикселя.

Эта процедура может быть распространена и на все изображение, однако пиксели, запрашивающие одинаковые координаты по значениям первой и второй цветовых составляющих, будут конкурировать друг с другом по записи. Преимущество отдается последнему запросу и информация о предыдущих запросах будет утеряна. Искусственно можно устранить этот недостаток проверкой тега запроса ячейки, и при наличии факта предыдущего запроса кодировать информацию в ячейке, например, формируя число в позиционной системе счисления с основанием, равным числу уровней квантования третьей цветовой составляющей пикселя +1 (для тега отсутствия запроса позиции). В дальнейшем мы будем допускать потерю части информации о предыдущих запросах.

На рис. 3.1 приведен вид зон существования объектов в RGB пространстве. В качестве исследуемого изображения принята комбинация поверхности горы и неба, т. е. двух классов.

Как видно, они образуют соприкасающиеся, достаточно компактные группы точек. Для сравнения на рис. 3.2 показано отображение цветового хаоса.

Матрица Z на рисунках заполнена по формуле

.

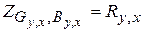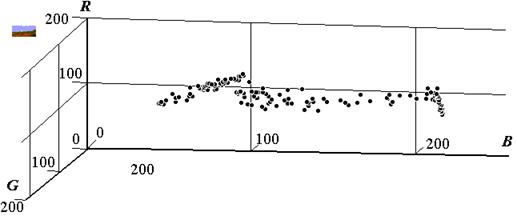
Рис. 3.1. Кластеры объектов в RGB пространстве

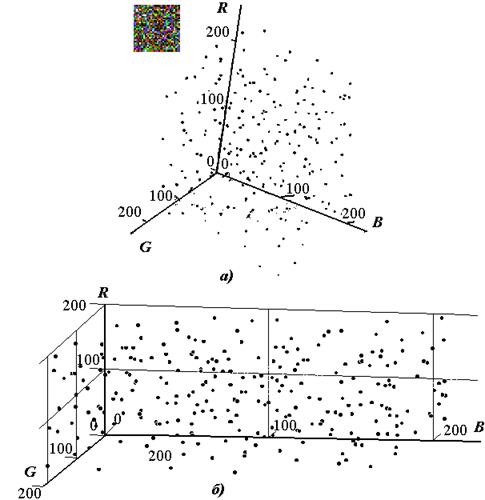
Рис. 3.2. Варианты отображение в RGB – пространстве цветового “хаоса”

Для упрощения в качестве тега отсутствия запроса ячейки принято число “0”, а информация о точках с 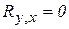утеряна. Имеет место и маскирование пикселями с 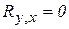предыдущих записей.

В качестве решающих границ в трехмерном пространстве описания пикселей используются различные поверхности. Более просто, но с определенной потерей общности анализа, можно учитывать только следы точек на координатной плоскости (рис. 3.3). В этом случае решающие границы вырождаются в линии, которые разделяют следы точек на плоскости.

Простейшие задачи распознавания решаются сечением пространства признаков плоскостями, которые разделяют зоны описаний классов. Например, через задание порогов по R, G, B компонентам (рис. 3.4 пороги rs, gs, bs). В этом случае говорят о гиперконусе принятия решений. Назначая нижние и верхние границы существования классов, получим прямоугольную область существования объектов класса. Однако многие ситуации значительно сложнее, и решающие функции приобретают вид сложных гиперповерхностей.

Сформируем прозрачную маску mask1 на распознаваемое здание (код 255 назначим прозрачным цветом, такое решение часто используется в графических редакторах)

.

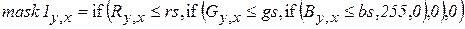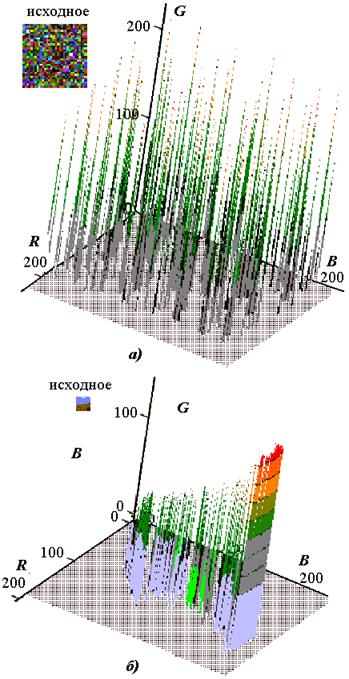
Рис. 3.3. Следы отображений пикселей на плоскости RB

Автоматическое задание фиксированных порогов по цветовым составляющим предполагает наличие алгоритмов определения уровня освещенности объектов. Но освещенность отдельных фрагментов объекта обычно значительно изменяется. Выходом может стать переход к распознаванию объектов в нормированном цветовом пространстве. На рис. 3.5 приведены нормированные сигналы r, g, b полученные из исходных сигналов R, G, B путем их деления на сумму R+G+B, вычисляемой для каждого пикселя.

Как и в первом случае сформируем прозрачную маску

.

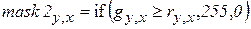Результаты вычислений представлены на рис. 3.6. Как видно, отдельные элементы здания распознаны различными алгоритмами не однозначно. Бесспорное преимущество второго метода в его независимости от освещенности объекта. Первый метод косвенно использует информацию об освещенности пикселя и этот признак в данном случае способствует лучшему распознаванию объектов.

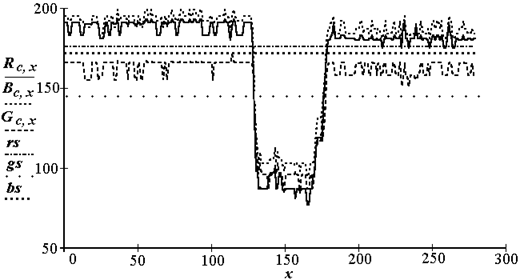
Рис. 3.4.. Сечения решающих плоскостей и сигналов от цветовых составляющих

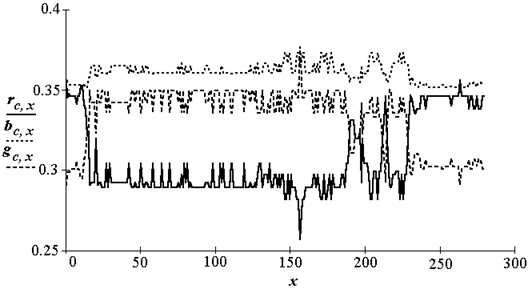
Рис. 3.5. Нормированные цветовые сигналы

Приведем перечень операций, часто используемый при распознавании объектов в нормированном цветовом пространстве:

· вычислим сумму цветовых сигналов в точке;

· определим нормированные цветовые составляющие;

· назначим исключаемую из рассмотрения нормированную цветовую составляющую (обычно не учитывают цветовую составляющую в равной мере присущую всем объектам);

· понизим размерность цветового пространства на единицу;

· назначим новые координатные оси;

Рис. 3.6. Примеры применения алгоритмов распознавания объекта:

а) – объект - строение на фоне неба; б) – маска mask1, вычисленная через проведение решающих плоскостей по уровням сигналов от цветовых составляющих, и результат ее наложения; в) – маска mask2, определенная по нормированным цветовым сигналам, и результат ее наложения

· отобразим следы объектов или их гистограммы в новой системе координат;

· проведем решающие границы и классифицируем объекты.

На рис. 3.7 показаны результаты проведения выше перечисленных операций для исходного трехцветного пространства. Нормирование понижает размерность пространства на единицу, в случае трехмерного пространства это означает переход к плоским отображениям, легко представляемым графически.

Так как нормированные цветовые сигналы используются в качестве индексов в новых массивах, описывающих цветовое пространство, и могут принимать только цельночисленные значения, умножим r, g на 100 и отбросим дробную часть числа:

;

.

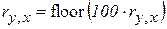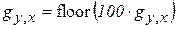Следы ZS и гистограмму Zhi на плоскости r0g получим по формулам:

;

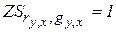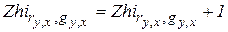(рис. 3.8 для следов).

Решающая функция из поверхности трансформируется в линию на плоскости, в данном случае параллельную оси 0g. Сформируем маску mask3 выделяющую гору.

.

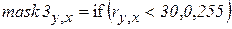На рис. 3.8 приведены маскированные распознанные объекты – часть горы и небо.

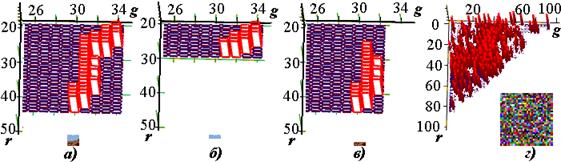
Рис. 3.7. Следы объектов на нормированной цветовой плоскости:

а) – гора и небо; б) – только небо; в) – только гора; г) – цветовой хаос

Рис. 3.8. Маски объектов в нормированной цветовой плоскости:

а) – гора и небо; б) – маскирована гора; в) – маскировано небо; г) – маска на небо; д) – маска на гору

Аналогичные рассуждения применимы и к виртуальным объектам – кодовым последовательностям, скрытой информации и т. п. Учет специфики данных объектов и назначения этих объектов и классов объектов, на фоне которых они проявляются, необходим.

Интерферометр по схеме интерферометра Майкельсона служит для измерения перемещений, ход лучей показан на рис.3.9.

Коллиматор позволяет уменьшить угловую расходимость лазерного излучения, обеспечивая постоянство диаметра интерферирующих пучков, конечно с определенны допуском. Отражатели выполнены в виде триппель призм, параметры которых приведены ниже. Период сигнала = 2π соответствует смещению каретки на λ/2, где λ – длина волны лазера в среде распространения (воздух) ~ 0,63 мкм.

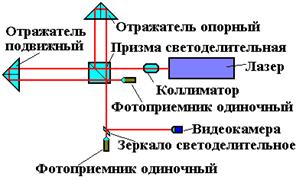
Рис. 3.9 Ход лучей в интерферометре

Видеокамера позволяет видеть и регистрировать распределение поля интерференции при низкоскоростных смещениях каретки, как фильмы. Фазасигналов в поле интерференции позволяет контролировать перемещение в единицах нанометра.

Обработка фильмов может производиться по миниатюрам (рис. 3.13 –опорный, рис. 3.10 –рабочий, рис. 3.11 –суммарный ).

Видеофайлы можно обрабатывать различными программными пакетами. Суммарный расчет по полю усреднит искомое значение смещения.

Рис. 3.10. Миниатюры с 16 кадров фильма от опорного сигнала ( )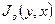

Для анализа необходимо выбирать только одноименные ( 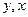) участки прямоугольного поля, в которых величины опорного и рабочего сигнала превосходят уровень шума в несколько раз. В каждой точке

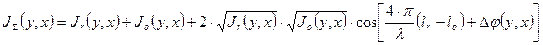
где 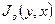, , 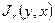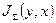значения опорного, рабочего и суммарного сигнала соответственно; 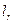, 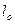- длинны рабочего и опорных плеч интерферометра; 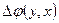- постоянная составляющая сдвига фаз в точке 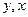, обусловленная юстировкой и дефектами деталей схемы.

Получение 2 первых файлов изображений необходимо для вычисления достоверных значений 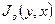, 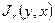путем усреднения полученных сигналов по кадрам (при каждой фиксации один из интерферирующих пучков перекрыт).

Отсутствие интерференции приводит к постоянству сигналов по полю.

Вторая цель расчетов – сформировать маску (распознать участки допустимые для анализа) для последующих расчетов фазы. У каждого из сигналов установите порог достоверности, например, 0.3 от его среднего значения в рабочей зоне.

Рис. 3.11. Миниатюры с 16 кадров фильма от рабочего плеча интерферометра ( )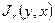

Рис. 3.12. Миниатюры с 64 кадров фильма от суммарного сигнала ( )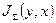

Вычислите маску, например, единичную по “И”, в которой оба сигнала достоверны и могут принять участие в расчетах.

Обработка суммарного сигнала с учетом масок распознанных позволяет получить нано метровое разрешение рис.3.13.

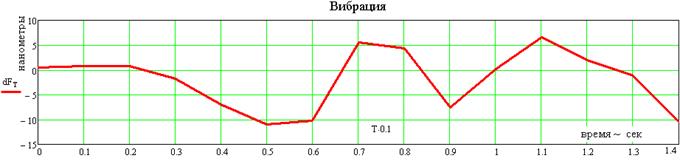
Рис. 3.13. Результат расчетов по видеофайлам суммарного потока)