Точное определение геометрических параметров

Поясним последовательность и специфику операций на примере. Пусть требуется определить координату по строке и размер объекта, приведенного на рис. 2.15. Там же прорисован вид сигнала по строке, выделенной на изображении черной линией.

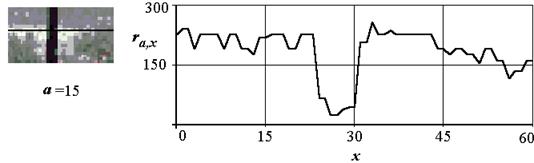
Рис. 2.15. Объект на естественном фоне

Вначале выделим объект (по априорным данным его ширина >= 7 пикселям). Введем фильтр F1 (рис.2.16) и профильтруем данные массива r по строке a. Выходной сигнал f1 (рис.2.17) найдем по формуле

;

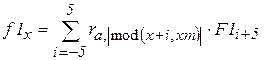где 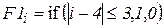, xm – размер строки, а операция взятия адреса точки на строке по модулю размера строки исключает выход за ее приделы.

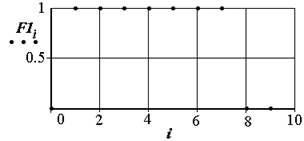
Рис. 2.16. Прямоугольный фильтр, селектирующий объекты по энергии

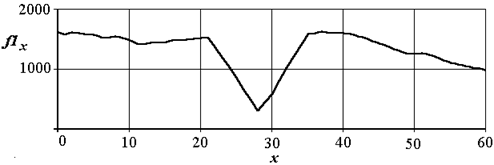
Рис. 2.17. Сигнал по строке после фильтрации

Как видно из графиков (рис. 2.15 и 2.17), улучшилось соотношение сигнал /шум. Оценить улучшение количественно можно оценив шум вне зоны сигнала и размах сигнала. Найдем si – соотношение сигнал/шум в децибелах для исходного и отфильтрованного сигналов по формуле

;

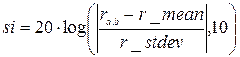где точка b – положение максимума сигнала, r_mean, r_stdev – оценки среднего и среднеквадратичного отклонения на участке, предшествующем сигналу. Расчеты показали увеличение si после фильтрации практически на 7 децибел.

По положению минимума не сложно оценить приближенно координату объекта x_grubo. Для более точного расчета изменим форму фильтра (рис.2.18), формулу свертки оставим прежней.

.

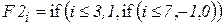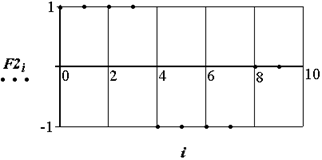
Рис. 2.18. Прямоугольный фильтр для поиска координаты объекта

Выходной сигнал f2 представлен на рис.2.19. На рисунке изображен сигнал по полной строке и на ее участке в зоне пересечения нуля. Точка пересечения сигналом нуля является точкой, в которой сумма участка исходного сглаженного сигнала в положительном крыле фильтра равна сумме в отрицательном крыле фильтра, т. е. фильтр делит сигнал на две равные по сумме составляющие и данная точка является искомой координатой.

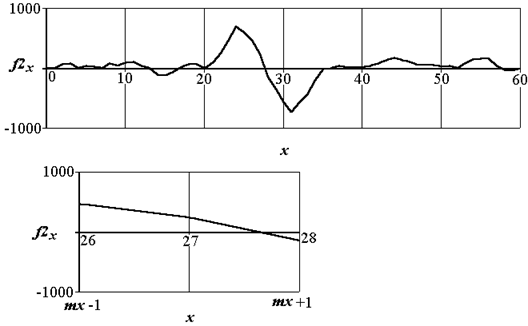
Рис. 2.19. Выходной сигнал при поиске координаты объекта

Уточним оценку координаты в зоне x_grubo используя линейную интерполяцию

;

;

;

.

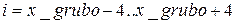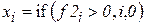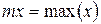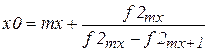Новая оценка координаты – x0 = 27.6.

Для определения размера приблизим форму фильтра к форме второй производной от фронта сигнала. Математические пакеты позволяют таблично задать вектор, введем

F3={0, 0, 0, 1, -1, 0, 0, 0, 0, 0, 0}

(форма фильтра изображена на рис. 2.20), и вычислим свертку (выходной сигнал - на рис.2.21).

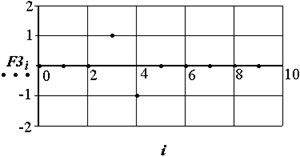
Рис. 2.20. Цифровой фильтр для определения размера

доминирующего объекта

Расстояние между положениями максимума и минимума по оси x в выходном сигнале равно 7, это и есть искомый размер.

Рис. 2.21. Выходной сигнал при оценке ширины объекта

Приведенные выше фильтры являются квазиоптимальными. Для линейных алгоритмов определения координат, размеров объектов,

они дают достаточно хорошие результаты.

Более корректное решение предполагает распознавание формы сигнала, оценку его параметров, генерацию эталонного сигнала полученной формы, получение разностного сигнала при смещении эталонного вдоль распознаваемого и определение положения эталонного, при котором минимизируются штрафы за ошибки в оценке координат, размеров.

По сути, процедура решения задач распознавания объекта часто подобна раскрытию матрешки. Определившись с одним объектом для распознавания, Вы обнаруживаете задачу распознавания его компонентов и т. д. Описав геометрию объекта, необходимо распознать форму границы объекта, составить описания классов помех во всех случаях и т. п., распознать границу, определить грубо ее положение и уточнить координаты.

Наряду с анализом признаков одиночных объектов, часто требуется определить геометрические признаки и для групповых объектов. К ним относятся средние величины расстояний, средние размеры объектов, входящих в группу.