Статистическая обработка полученных образов

Определим центральные моменты, назначим число каналов анализа (например 100), положение канала на оси th и найдем функцию гистограммы rh (например, для составляющей R выбранного сегмента):

,

,

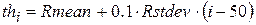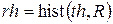где Rmean, Rstdev – оценки математического ожидания и среднеквадратичного отклонения составляющей R изображения в сегменте.

Ниже на рис. 1.3 приведены параметры гистограмм для сегментов и на рис. 1.4 – их вид.

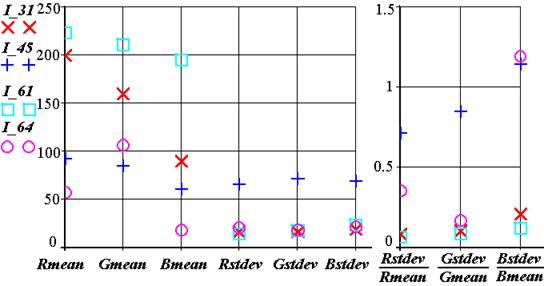
Рис. 1.3. Параметры гистограмм r, g, b:

Rmean, Gmean, Bmean оценки величин математических ожиданий составляющих R, G, B;

Rstdev, Gstdev, Bstdev оценки величин среднеквадратичных отклонений составляющих;

R, G, B; I_31, I_61, I_45, I_64 значения оценок указанных центральных моментов для шляпки, ножки гриба, для неоднородного и квазиоднородного фона

В приведенном примере не обосновывается выбор количества каналов, метрика оси параметра th для простоты принята линейной. В ряде практических случаев такие упрощения не допустимы. Доверительный интервал оценки показаний канала гистограммы зависит от его показаний, общего числа опытов.

Визуально ошибки в выборе положения и размера канала видны по изрезанности полученных кривых, в явном превышении показаний отдельных каналов над показаниями остальных и т. п.

По полученным гистограммам принимается решение о виде закона распределения и о его параметрах. Наиболее часто гистограммы анализируются по их виду на близость к известным функциям плотности вероятности.

Рассмотрим эти процедуры, ориентируясь на терминологию теории распознавания. Описание классов, к одному из которых следует отнести исследуемую гистограмму, задано аналитическими выражениями. На рис. 1.5 приведены примеры функций плотностей вероятности, имеющихся в перечне стандартных функций. Необходимо определить потери (или выигрыш) от отнесения полученных гистограмм к заданным классам и принять решение о принадлежности конкретной гистограммы к одному из них.

Для наглядности покажем результаты сравнения на искусственном примере. Сравним результат генерации случайных чисел в среде математического пакета с теоретической кривой плотности вероятности (в примере – плотность нормального распределения).

Сформируем вектор случайных чисел s, распределенных по нормальному закону с параметрами: математическое ожидание Mean, среднеквадратичное отклонение Stdev и числом элементов вектора im (в примере im = 1000).

.

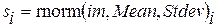Построим гистограмму px при числе каналов, равном 40, и вызываем функцию нормального распределения p с теми же параметрами (рис. 1.5): j = 1..40; ; ; .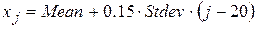

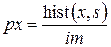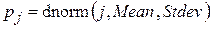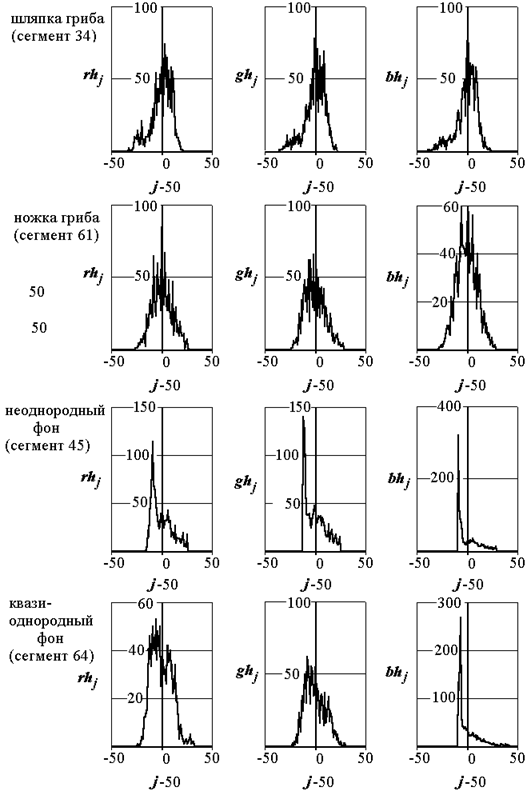
Рис. 1.4. Гистограммы rh, gh, bh для выделенных объектов

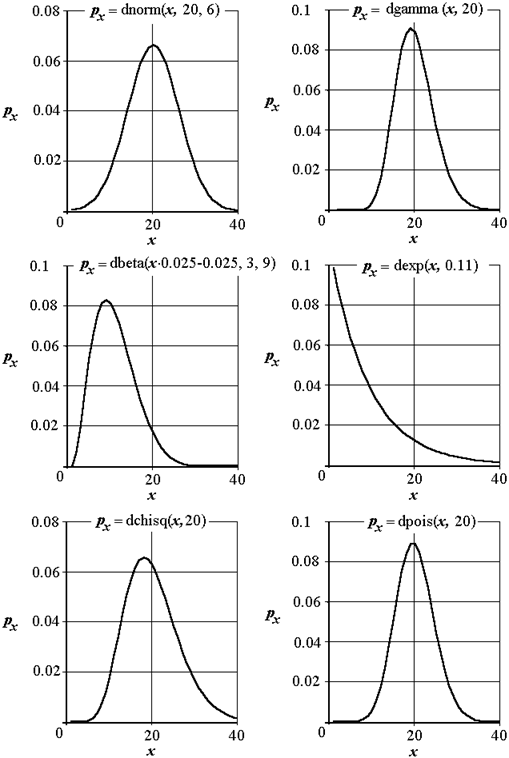
Рис 1.5. Генерация функций плотности распределения

Разность теоретических и практических результатов приведена на рис. 1.6. По этим данным можно оценить потери от использования выбранного закона распределения.

Величины потерь очень часто описываются симметричными относительно нуля функциями, например:

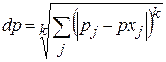, где k – показатель степени, определяющий метрику оси отклонений.

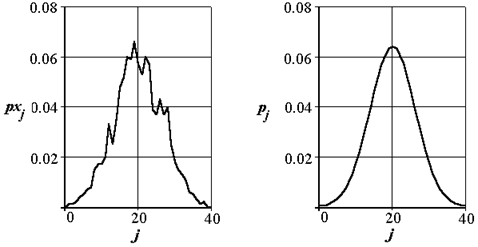
Рис 1.6. Гистограмма px и кривая плотности нормального распределения

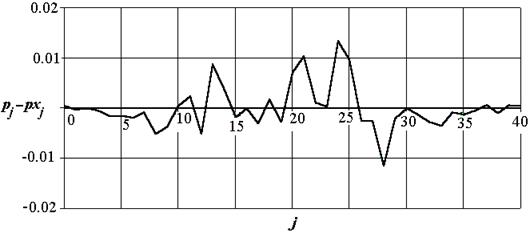
Рис 1.7. Разность экспериментально полученной гистограммы и теоретической кривой

При k = 2 (принятие решения по min среднеквадратичного отклонения), для нашего случая dp = 0.05.

В практике распознавания широко используется представление описаний классов в производных пространствах. В данной лабораторной работе рассматривается поиск отличительных признаков объектов в области пространственных частот. На рис. 1.8 представлены - модуль частотного спектра неоднородного сегмента (45) и его сечение. Вызов функции преобразования Фурье, как правило, затруднений не вызывает. Однако переход к пространственным частотам не всегда очевиден. Для приобретения навыков работы с Фурье-образом рекомендуется сформировать изображение с гармонически изменяющейся яркостью и детально проанализировать метрику осей пространственных частот.

Например: задав размеры изображения в координатах j и i, вызовите функцию Im1 периодом T и амплитудой A<127.5. Выполните преобразование Фурье и определите масштабы осей пространственных частот. .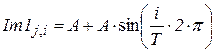

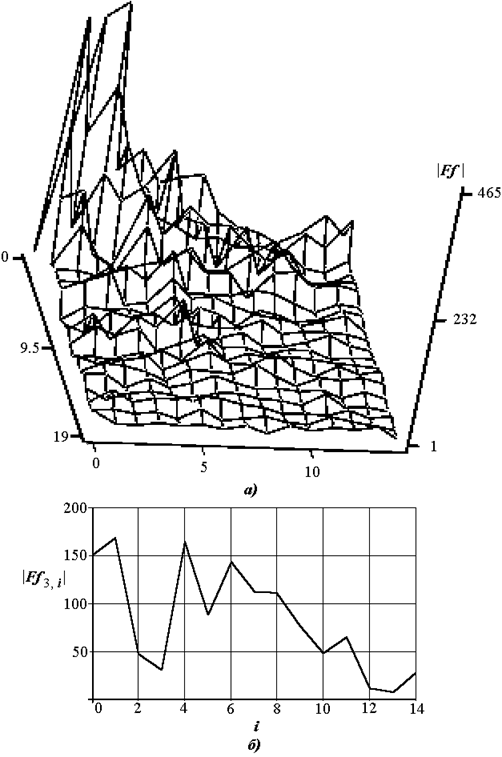
Рис. 1.8. Фурье-образ R – составляющей сегмента неоднородного фона