Упрощенное определение геометрических параметров

Данная операция широко используется в системах обнаружения, как первая процедура при локализации объектов. Полное решение задачи распознавания, как правило, содержит много процедур, в дальнейшем часть из них будем опускать, останавливаясь только на ключевых. Рассмотрим простейший пример. Пусть необходимо распознать объекты (лодки) по площади их бортов. На рис.2.11приведено изображение борта лодки и сигнал по столбцу с номером 212, взятый из анимационного фильма, показывающего изменение видеосигнала при смещении анализируемого столбца по кадру. На нем отчетливо виден всплеск сигнала при переходе от светового сигнала с водяной поверхности на борт лодки и спад сигнала в зоне перехода с борта лодки на водяную поверхность. Анализ сигналов показывает возможность определения площади борта как сумму расстояний по столбцам от первого яркостного всплеска до последнего провала сигнала (по границам контуров борта лодки).

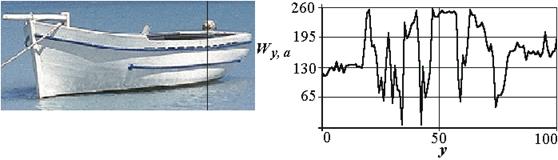
Рис. 2.11. Изменения сигнала по выделенному черной линией столбцу

Зададим пороги яркости – 220 и 70 (встреча с бортом и с тенью от борта). Зададим координату по y – 50. Эта величина будет использована для ограничения зоны встречи с бортом. В столбцах, в которых процедуры не обнаружили наличие борта вставим 255. Из исходного массива W сформируем (с учетом порогов) рабочие массивы WH, WL. Найдем минимум и максимум по столбцам и скорректируем полученные данные, устранив недостоверные результаты. На рис. 2.12приведены выходные функции.

;

;

;

;

;

;

;

;

;

.

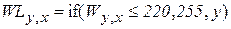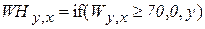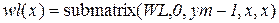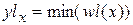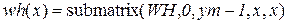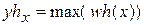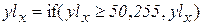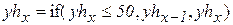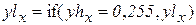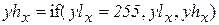Разностная функция (рис. 2.12 в) показывает высоту борта лодки. Найдем интеграл от нее по x:

.

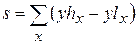Расчет дает s = 11470квадратных пикселей, это и есть грубая оценка площади борта лодки.

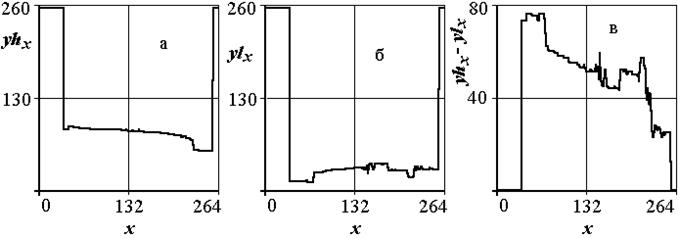
Рис. 2.12. Определение площади по границам контуров

Второй пример: определение местоположения объектов, выделяющихся из общего фона по яркости (рис. 2.13). Зададимся минимальными размерами объектов по x – xs=15, по y – ys=5. Сформируем сегмент с указанным размером и переместим его с шагом по x и y равным единице от начала до конца изображения, вычисляя каждый раз среднее значение сигнала в сегменте d (рис. 2.14).

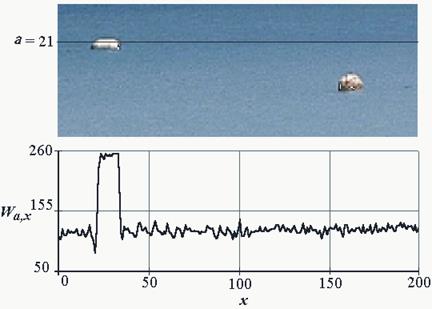
Рис. 2.13. Локация объектов

Такой прием позволяет увеличить соотношение сигнал/шум и надежнее распознать объекты по энергии сигнала. Координата максимума jm (номер сегмента) показывает положение наиболее освещенного объекта. Переведем ее в физические координаты объекта на изображении yo, xo:

;

;

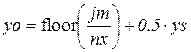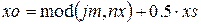где nx – число сегментов в строке. Расчеты в приведенном примере показали оценки координат первого объекта yo = 22.5и xo = 26.5. Продолжая поиск максимума вне зоны обнаруженного объекта по описанной методике получаем оценки координат второго объекта yo = 42.5 и xo = 168.5. Более корректное выполнение операций поиска координат требует проведения низкочастотной фильтрации сигнала в сегменте для устранения тренда, обусловленного конкретным положением источника света.

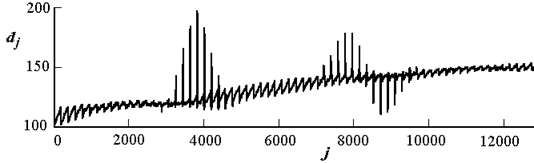
Рис. 2.14. Бегущее среднее значение сигнала в сегменте