Общие сведения. Назначение признака элементом алфавита признаков сопровождается присвоением ему коэффициента значимости

Назначение признака элементом алфавита признаков сопровождается присвоением ему коэффициента значимости, обычно за 1 принимается значимость наиболее мощного признака (при вычислениях в целых числах для уменьшения времени расчетов верхнее значение будет равно 255).

Признаки выбираются итерационной процедурой, исходя из априорных сведений об объектах, фоне и результатах сравнения перекрытий описаний классов. Сравнение проводится при отсутствии корреляции между признаками на числовой оси признака или в гиперпространствах коррелированных признаков.

Понижение размерности исследуемого пространства признаков – классическая задача в теории распознавания. В технических приложениях ее сводят к задаче построения преобразующего фильтра, выходной вектор сигнала которого имеет заметно меньшую размерность, чем входной вектор. Классификация в пространстве меньшей размерности выполняется быстрее и проще.

В технике наиболее распространенным принципом понижения размерности является преобразование исследуемого пространства в пространство базисных функций (тригонометрических, экспоненциальных, дельта функций). Выбор типа базисных функций основывается на понятии расстояния между различаемыми классами в новых пространствах. Важную роль играют априорные сведения об исследуемых объектах. При достаточном объеме данных можно решать задачу так, чтобы, сохранив вероятность правильного принятия решения о принадлежности объекта к собственному классу, получить новое описание в базисных функциях минимального размера.

Практически правило сжатия гиперпространства базисных функций, содержащего образ исходного вектора, может быть сформулировано для случая непересекающихся классов следующим образом:

· сжатие допустимо до тех пор, пока не пересекутся крайние точки доверительных интервалов классов, дополненные доверительными зонами крайних объектов в соседних классах (рис. 2.1).

В исходном описании изображений первой процедурой обычно является процедура укрупнения пикселя. Если отсутствует отработанный алгоритм описания классов в пространстве признаков, то целесообразно ее проводить почти до уровня сохранения различия объектов на изображении при решении принимаемом человеком. Данная процедура проводится и в пространствах базисных функций, например, в Фурье-отображениях сегментов. В простейшем случае укрупнение пикселя – это выборка с массива отсчетов в массив меньшей размерности. Ниже приведена процедура формирования массива RQ из R. Размерность нового массива в my × mx меньше, чем исходного. На рис. 2.2 показаны изображения до и после сжатия (левый верхний угол). Возможность распознавания объектов не потеряна. Это подтверждает и вид сигналов снятых с одних и тех же участков изображений (рис. 2.3).

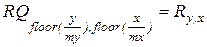
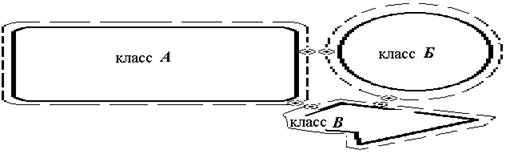
Рис. 2.1. Сжатие описаний пространства признаков до соприкосновения доверительных интервалов границ классов (А и В)

Более корректно операция укрупнения пикселя проводится через сегментацию и идентификацию мини объектов внутри сегмента (например, при распознавании чертежей не уничтожаются последние пиксели линий).

Рис. 2.2. Укрупнение пикселя в 4 раза по х и примерно в 8 раз по у

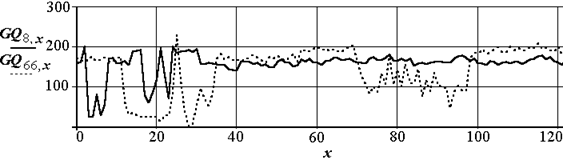
Рис. 2.3. Сигналы: после сжатия – строка 8 и до сжатия – строка 66

Следующая процедура – уменьшение размерности описания пикселя. Обычно исходное описание в 3-цветной модели имеет размер 24, 30, 48 бит в зависимости от разрядности систем оцифровки аналоговых сигналов.

Уменьшение разрядности линейным, нелинейным масштабированием сигналов цвета или адаптивным выбором цветов, сохраняющих межклассовую специфику объектов, позволяет снизить объем описания пикселя в несколько раз. На рис. 2.4-2.8 показаны результаты выполнения этапов уменьшения разрядности описания пикселя.

На первом этапе находятся гистограммы R, G, B составляющих (рис. 2.4).

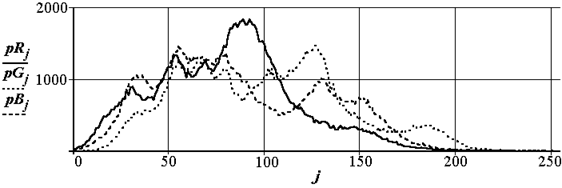
Рис. 2.4. Гистограммы R, G, B составляющих изображения кисти винограда

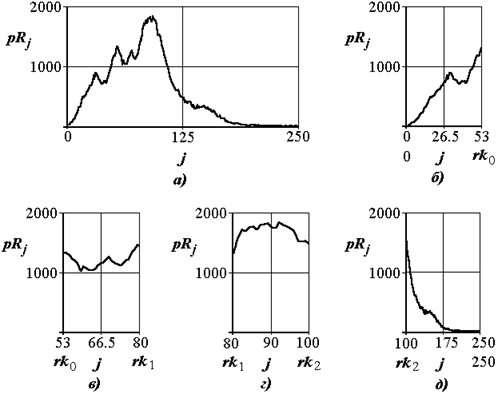
Рис. 2.5. Выделенные участки гистограммы R составляющей:

а) вся зона, б), в), г), д) зоны содержащие одинаковое число пикселей

Далее задается правило разбиения осей на участки (исходное описание 8 бит – на составляющую).

В нашем случае отработано 2 алгоритма с преобразованием 2-3-2 т. е. 7-битном и 1-2-1 т. е. 4-битном представлении выходного описания пикселя. Результат разбиения оси R на четыре участка с равным количеством пикселей отображен на рис. 2.5. Границы участков служат уровнями логических компараторов, перекодирующих описание пикселей.

На рис. 2.6 и 2.7 приведены графики формирования выходного кода k по уровням R, G, B составляющих.

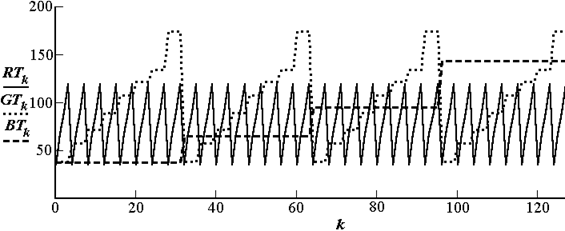
Рис. 2.6. Графики перекодировки RGB описания пикселя (возвращается k) для выходного описания 2-3-2 бита

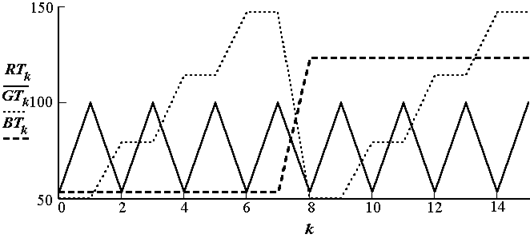
Рис. 2.7. Графики перекодировки RGB описания пикселя (возвращается k) для выходного описания 1-2-1 бит

На рис. 2.8 показан результат перекодировки 24 бита в 7 бит без потери различия объектов. В варианте 24 в 4 бита часть объектов стали неразличимы.

Предельным вариантом сжатия является бинаризация описания, т. е. представление яркости и цвета пикселя нулем или единицей. Выбор порога в бинаризации достаточно сложная процедура. В простейшем случае величина порога задается фиксированной по всему полю изображения. На рис. 2.9 показаны сигнал по строке и результат бинаризации изображения текста низкого качества при величине порога rs = 117. Отдельные элементы букв утеряны (буква "н" в 6 строке не отличается от буквы "п") или стали не различимы по направлению элементов (ряд букв "и" в 4, 5 строке не различимы от буквы "н") и т. п.

Рис. 2.8. Изображение кисти темного винограда на фоне листвы:

а) до перекодировки; б) после перекодировки; в) новая палитра (2-3-2)

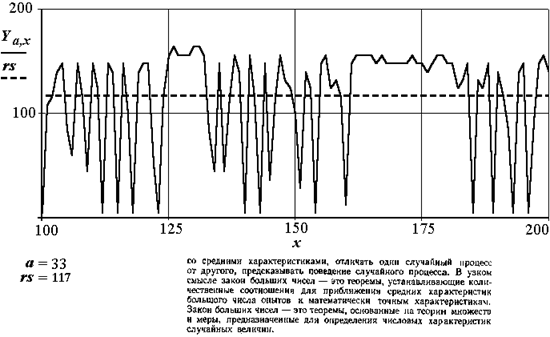
Рис. 2.9. Бинаризация изображения низкого качества с фиксированным порогом

Несколько лучшие результаты получаются при плавающей по полю величине порога. Она может выбираться в процентах от усредненного сигнала в сегменте, средним элементом которого является бинаризуемый пиксель. Величина процента также может быть адаптивно изменяемой, в зависимости от типа сегмента, места пикселя в сегменте и т. п. Например, если W – исходное изображение , w – бинаризованное изображение, y, x – координаты бинаризуемый точки, xs, ys – размеры сегмента, hx, hy – шаг смешения сегмента, nx – число сегментов по x, то правило бинаризации можно записать следующим выражением:

,

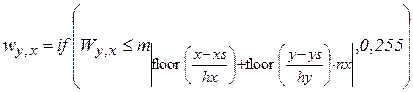где 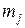– среднее, медиана или мода j-го сегмента. На рис. 2.10 показан результат бинаризации изображения текста с ys=30, xs=20, hy=20, hx=20, nx=18 и .

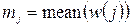Рис. 2.10. Бинаризация изображения низкого качества с плавающим порогом