На линейные и квадратичные множители.

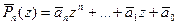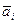Определим для P_n (z) многочлен , где - число, комплексно сопряженное коэффициенту a_i . При этом 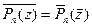. Следовательно, если z₀ – корень P_n , то 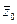- корень 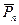. Если коэффициенты P_n – действительные числа, то 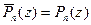, и если z₀ = a + ib – его корень кратности k, то 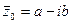- тоже его корень, причем той же кратности. Но 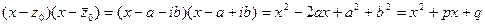- квадратный трехчлен с отрицательным дискриминантом. Если теперь применить к многочлену с действительными коэффициентами от действительной переменной P_n (x) формулу (8.2), то

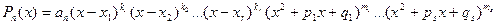(8.3)

то есть всякий многочлен на множестве действительных чисел можно разложить на множители степени не выше второй.