Линейные дифференциальные уравнения 1 порядка
Линейные дифференциальные уравнения это вида 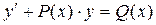 , где P(x), Q(x) – непрерывные функции.
, где P(x), Q(x) – непрерывные функции.
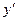 и
и 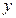 входят в уравнение линейно, т.е не перемножаются между собой.
входят в уравнение линейно, т.е не перемножаются между собой.
 Сделаем замену:
Сделаем замену: 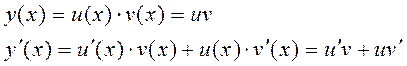

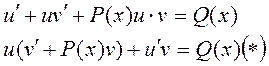
Приравняем скобку к 0
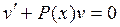 подставим
подставим 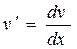
 - дифференциальное уравнение с разделяющимися переменными.
- дифференциальное уравнение с разделяющимися переменными.
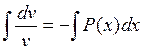
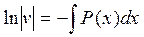 константу интегрирования не прибавляем, т.к достаточно одного частного решения.
константу интегрирования не прибавляем, т.к достаточно одного частного решения.
Выразим явно 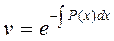
Подставим 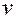 в (*)
в (*) 
Выразим 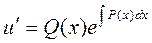
Т.к  , то проинтегрируем обе части последнего уравнения по х
, то проинтегрируем обе части последнего уравнения по х
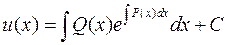
Общее решение линейного уравнения:
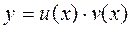 - всегда получается в явном виде.
- всегда получается в явном виде.
Пример: 
1) 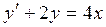
 2)
2) 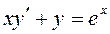 y(1)=2
y(1)=2
Дата добавления: 2015-01-09; просмотров: 965;
