Дифференциальные уравнения 2 порядка, допускающие понижение порядка
 1) Уравнения вида:
1) Уравнения вида: 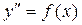
уравнение решается двукратным интегрированием по переменной х.
Проинтегрируем 1 раз по х.
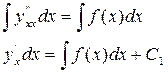
Проинтегрируем 2 раз по х
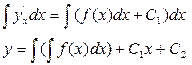
общее решение.
Замечание: для дифференциального уравнения порядка n: 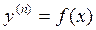 - интегрировать нужно n раз.
- интегрировать нужно n раз.
Примеры:
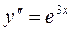
2) Дифференциальные уравнения не содержащие явно y.

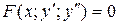 - нет явно y
- нет явно y
Замена 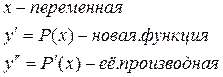
Подставим замену в дифференциальное уравнение, получим 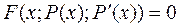
получим дифференциальное уравнение 1 порядка.
Найдём решение этого уравнения:
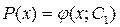
сделаем обратную замену 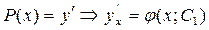
 проинтегрируем обе части по х
проинтегрируем обе части по х 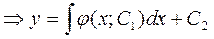 - общее решение
- общее решение
Пример:
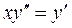
3) Дифференциальные уравнения 2 порядка не содержащие явно х.
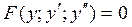 - нет явно х.
- нет явно х.
 Замена: у-новая переменная
Замена: у-новая переменная
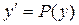 - новая функция
- новая функция
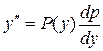 - её производная
- её производная
Подставим замену в исходное уравнение
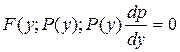
получим дифференциальное уравнение 1 порядка:
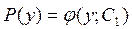 - его решение
- его решение
Сделаем обратную замену - 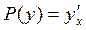
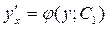 - дифференциальное уравнение с разделяющимися переменными. Разделим переменные:
- дифференциальное уравнение с разделяющимися переменными. Разделим переменные:
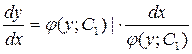
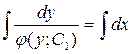 ;
; 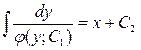 - общее решение (вид неявный)
- общее решение (вид неявный)
Примеры:
1. 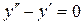
2. 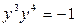
Дата добавления: 2015-01-09; просмотров: 1271;
