Теорема Коши.

Если функция 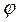в (*) непрерывна вместе с частными производными:

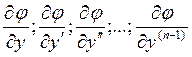в области содержащей значения

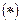, то существует единственное решение дифференциального уравнения удовлетворяющее начальным условиям:

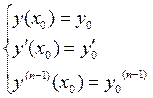
Замечание: для дифференциальных уравнений 2 порядка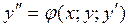

начальные условия имеют вид:

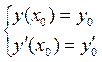
Решить дифференциальное уравнение порядка n означает:

1)Найти общее решение (общий интеграл)

2)Найти частное решение (частный интеграл), удовлетворяющее заданным условиям.

Определение:Общим решением дифференциального уравнения 2 порядка

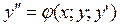является функция 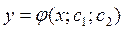, такая что:

1) при любых значениях с₁ и с₂ эта функция – решение.

2) каковы бы ни были начальные условия на области, в которой выполняется теорема Коши всегда можно подобрать значения с₁ и с₂ удовлетворяющие начальным условиям.

Определение:Частным решением дифференциального уравнения 2 порядка является решение, при конкретных значениях с₁ и с₂.

Замечание: общее решение дифференциального уравнения 2 порядка может быть получено в неявном виде: