Дифференциальные уравнения высших порядков. Задача Коши. Понятие о краевых задачах для дифференциальных уравнений. Уравнения, допускающие понижение порядка.

Рассмотрим дифференциальное уравнение п-го порядка:

F (x, y, y′,…, y⁽ⁿ⁾) = 0, (18.1)

где F предполагается непрерывной функцией всех своих аргументов. Тогда по теореме о существовании неявной функции (см. лекцию ) можно разрешить это уравнение относительно старшей производной:

у^(п) = f (x, y, y′,…, y^(n-1)) (18.2)

и сформулируем для него (без доказательства) теорему существования и единственности решения:

Теорема 18.1. Существует единственное решение уравнения (18.2), удовлетворяющее условиям

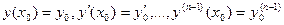,(18.3)

если в окрестности начальных значений (х₀ , у₀ , у′₀,…,у₀^(п-1)) функция f является непрерывной функцией всех своих аргументов и удовлетворяет условию Липшица по всем аргументам, начиная со второго.

Замечание 1. Так же, как и для дифференциального уравнения 1-го порядка, задача отыскания решения уравнения (18.2), удовлетворяющего условиям (18.3), называется задачей Коши.

Замечание 2. Теорема 18.1 утверждает существование частного решения уравнения (18.2), удовлетворяющего данным начальным условиям. С геометрической точки зрения это соответствует существованию интегральной кривой, проходящей через точку 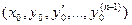. Но, используя эту теорему, можно доказать и существование общего решения уравнения (18.2), содержащего п произвольных постоянных и имеющего вид:

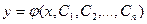(18.4)

или, в неявной форме:

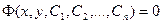. (18.5)

Соотношение (18.5) будем называть общим интегралом уравнения (18.1) или (18.2).