Уравнения, допускающие понижение порядка.

В некоторых случаях порядок дифференциального уравнения может быть понижен, что обычно облегчает его интегрирование. Рассмотрим несколько типов подобных уравнений.

1. Уравнение не содержит искомой функции и ее производных по порядок (k – 1) включительно:

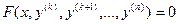. (18.6)

В этом случае можно сделать замену р = у^(k), которая позволяет понизить порядок уравнения до n – k, так как после замены уравнение примет вид

.

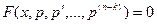Из этого уравнения можно найти р = р (х, С₁ , С₂ ,…, С_n-k), а затем найти у с помощью интегрирования k раз функции р = р (х, С₁ , С₂ ,…, С_n-k).

Пример.

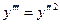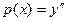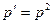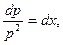
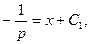
Уравнение при замене становится уравнением 1-го порядка относительно р: , откуда 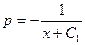. Тогда

.

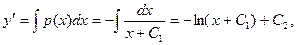
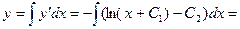
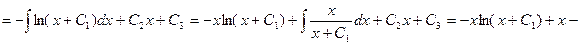
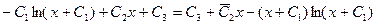2. Уравнение не содержит независимой переменной:

F ( y, y′,…, y⁽ⁿ⁾) = 0. (18.7)

Порядок такого уравнения можно понизить на единицу заменой у′ = р(у). При этом производные функции f(x) по аргументу х нужно выразить через производные р по у:

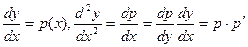и т.д.

Пример.

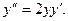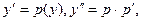Пусть тогда 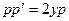. Отметим частное решение р = 0, то есть 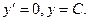Если 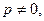после сокращения на р получим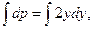

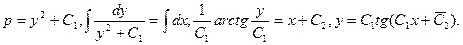
3. Уравнение F (х, y, y′,…, y⁽ⁿ⁾) = 0 однородно относительно аргументов y, y′,…, y⁽ⁿ⁾, то есть справедливо тождество

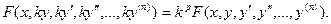
В этом случае можно понизить порядок уравнения на единицу, вводя новую неизвестную функцию z, для которой 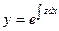. Тогда 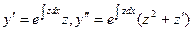и т.д.