Линейные неоднородные уравнения.

Ранее было показано (см. лекцию 19), что сумма решений линейного неоднородного уравнения L[y] = f(x) и соответствующего однородного уравнения L[y] = 0 является решением неоднородного уравнения. Используя это свойство, можно доказать следующую теорему:

Теорема 21.1. Общее решение на отрезке [a,b] уравнения L[y] = f(x) с непрерывными на [a,b] коэффициентами p_i(x) и правой частью f(x) равно сумме общего решения 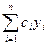соответствующего однородного уравнения и какого-либо частного решения неоднородного уравнения.

Доказательство.

Требуется доказать, что для любых начальных условий 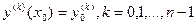, можно подобрать такие значения постоянных c_i, чтобы функция

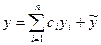, (21.5)

где y_i – линейно независимые частные решения однородного уравнения L[y] = 0, а - частное решение рассматриваемого неоднородного уравнения, была решением этого неоднородного уравнения с заданными начальными условиями. Это требование приводит нас к системе уравнений относительно неизвестных с₁, с₂,…, с_п:

, (21.6)

главным определителем которой является определитель Вронского 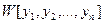, как известно, не равный нулю. Поэтому система (21.6) имеет единственное решение, что и доказывает утверждение теоремы.

Замечание. Таким образом, при найденном общем решении однородного уравнения решение неоднородного уравнения сводится к подбору его частного решения.

Лекция 22.

Методы нахождения частного решения неоднородного линейного дифференциального уравнения (метод вариации произвольных постоянных, метод неопределенных коэффициентов и принцип суперпозиции).

Распространим метод вариации произвольных постоянных, рассмотренный в лекции 19 для решения линейного уравнения первого порядка, на линейные уравнения высших порядков. Будем искать решение неоднородного уравнения в виде . При этом требуется найти п неизвестных функций с₁(х), с₂(х),…, с_п(х), которые удовлетворяли бы только одному уравнению

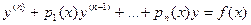. (22.1)

Поэтому можно дополнительно потребовать, чтобы искомые функции удовлетворяли еще каким-нибудь п-1 уравнениям, выбранным так, чтобы производные функции имели по возможности такой же вид, как при постоянных c_i. Первая производная решения имеет вид: 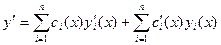. Потребуем, чтобы вторая сумма в этом выражении равнялась нулю: 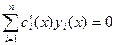, тогда 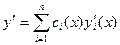. Зададим такое же условие для второй производной:

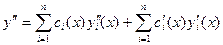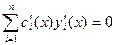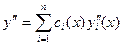, , . Продолжая вычислять производные функции до порядка п – 1 включительно и требуя каждый раз, чтобы 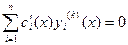, получим:

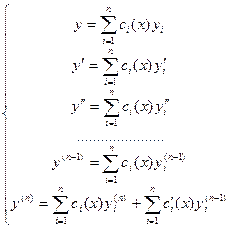(22.2)

( в последнем равенстве уже нельзя потребовать, чтобы вторая сумма равнялась нулю, так как на искомые функции уже наложено п – 1 условие, а последним требованием является то, что эти функции должны удовлетворять уравнению (22.1)). Подставив с учетом (22.2) в (22.1), получим:

,

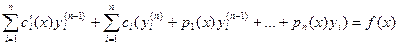но y_i – частные решения однородного уравнения, следовательно, все слагаемые второй суммы равны нулю и уравнение сводится к следующему: . (22.3)

Добавив его к первым п – 1 уравнениям системы (22.2), получим систему из п уравнений для определения с₁΄, с₂΄,…, с_п΄, определитель которой является определителем Вронского для функций у₁, у₂,…, у_п и, следовательно, не равен нулю. Следовательно, из этой системы можно единственным образом найти производные искомых функций, а затем с помощью интегрирования и сами функции с₁, с₂,…, с_п.

Пример.

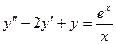. Найдем решение однородного уравнения, для чего составим характеристическое уравнение k² - 2k + 1 = 0, k₁ = k₂ =1. Следовательно, общее решение однородного уравнения имеет вид у = (с₁ + c ₂ x)е^х, то есть фундаментальную систему решений составляют функции у₁ = е^х и у₂ = хе^х. Будем искать общее решение неоднородного уравнения в виде у = с₁(х)е^х + с₂(х)хе^х. Составим систему (22.2):

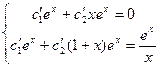, откуда ,

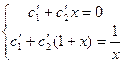, где С₁ и С₂ – произвольные постоянные. Таким образом, найдено общее решение исходного уравнения: у = е^х(хln|x| - x + C₁x + C₂).