Коэффициентами.
Для некоторых видов правой части линейного неоднородного дифференциального уравнения 
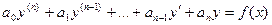 (22.4)
(22.4)
можно подобрать частное решение в виде функции с неопределенными коэффициентами, которые определяются путем подстановки этой функции в уравнение (22.4).
1. f(x) = A0 xs +A1 xs-1 +…+ As (ап ≠ 0). При этом существует частное решение уравнения (22.4), имеющее такой же вид: y = B0 xs + B1 xs-1 +…+ Bs. Действительно, подставив эту функцию в уравнение (22.4) и приравняв коэффициенты при одинаковых степенях х, получим разрешимую единственным образом систему линейных уравнений: 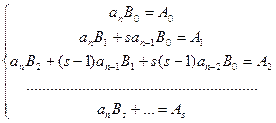 . Пример.
. Пример. 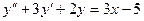 . Будем искать частное решение в виде у = Ах + В, тогда
. Будем искать частное решение в виде у = Ах + В, тогда 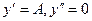 , и после подстановки в уравнение получим: 3А + 2Ах + 2В = 3х – 5. Тогда 2А = 3, 3А + 2В = = -5. Следовательно,
, и после подстановки в уравнение получим: 3А + 2Ах + 2В = 3х – 5. Тогда 2А = 3, 3А + 2В = = -5. Следовательно, 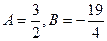 , и общее решение уравнения можно записать в виде:
, и общее решение уравнения можно записать в виде: 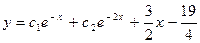 .
.
2. Если 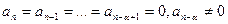 (то есть k = 0 является α – кратным корнем характеристического уравнения), то частное решение имеет вид:
(то есть k = 0 является α – кратным корнем характеристического уравнения), то частное решение имеет вид: 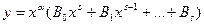 . Легко убедиться, что функция подобного вида является решением уравнения (22.4) при поставленных условиях. Пример.
. Легко убедиться, что функция подобного вида является решением уравнения (22.4) при поставленных условиях. Пример. 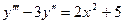 . Пусть
. Пусть 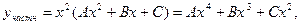
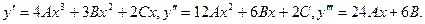 Подставляя в уравнение, получим:
Подставляя в уравнение, получим: 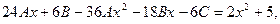 откуда –36А = 2, 24А – 18В = 0, 6В – 6С = 5. Решая эту систему, получаем
откуда –36А = 2, 24А – 18В = 0, 6В – 6С = 5. Решая эту систему, получаем 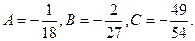 Следовательно, общее решение уравнения имеет вид:
Следовательно, общее решение уравнения имеет вид: 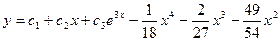 .
.
3. 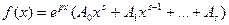 . Если число р при этом не является корнем характеристического уравнения, можно задать частное решение в виде:
. Если число р при этом не является корнем характеристического уравнения, можно задать частное решение в виде: 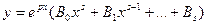 . Если же р – корень характеристического уравнения кратности α, частное решение имеет вид:
. Если же р – корень характеристического уравнения кратности α, частное решение имеет вид: 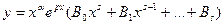 . В обоих случаях с помощью подстановки в исходное уравнение можно убедиться, что выбранные функции являются его решениями. Пример 1.
. В обоих случаях с помощью подстановки в исходное уравнение можно убедиться, что выбранные функции являются его решениями. Пример 1. 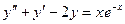 . Найдя корни характеристического уравнения k² + k – 2 = 0: k1 = 1, k2 = -2, видим, что р = -1 не является корнем этого уравнения. Поэтому будем искать частное решение в форме y = e-x(Ax + B). При этом
. Найдя корни характеристического уравнения k² + k – 2 = 0: k1 = 1, k2 = -2, видим, что р = -1 не является корнем этого уравнения. Поэтому будем искать частное решение в форме y = e-x(Ax + B). При этом 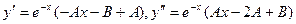 . Подставляя в уравнение, получаем:
. Подставляя в уравнение, получаем: 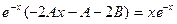 , откуда –2А = 1, -А – 2В = 0, то есть
, откуда –2А = 1, -А – 2В = 0, то есть 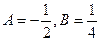 . Итак, общее решение уравнения:
. Итак, общее решение уравнения: 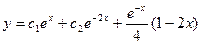 . Пример 2.
. Пример 2. 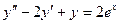 . Здесь р = 1 – корень характеристического уравнения кратности 2, поэтому частное решение имеет вид
. Здесь р = 1 – корень характеристического уравнения кратности 2, поэтому частное решение имеет вид 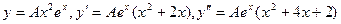 . Подстановка в уравнение дает 2Аех = 2ех, откуда А =1, а общее решение: у = (с1 + с2х + х²)ех.
. Подстановка в уравнение дает 2Аех = 2ех, откуда А =1, а общее решение: у = (с1 + с2х + х²)ех.
4. В аналогичной форме задаются частные решения в случае, когда правая часть уравнения (22.1) имеет вид 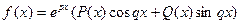 , где Р и Q – некоторые многочлены: а) если p ± qi - не корни характеристического уравнения, то можно подобрать частное решение в виде
, где Р и Q – некоторые многочлены: а) если p ± qi - не корни характеристического уравнения, то можно подобрать частное решение в виде 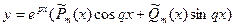 , где
, где 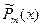 и
и 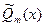 - многочлены с неопределенными коэффициентами, степень т которых есть старшая из степеней многочленов Р и Q.
- многочлены с неопределенными коэффициентами, степень т которых есть старшая из степеней многочленов Р и Q.
б) если p ± qi - корни характеристического уравнения кратности α, то
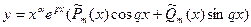 .
.
Пример.
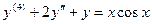 . При этом ±
. При этом ± 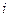 - корни характеристического уравнения кратности 2, поэтому следует искать частное решение в виде:
- корни характеристического уравнения кратности 2, поэтому следует искать частное решение в виде: 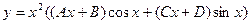 .
.
5. Если правая часть уравнения (22.1) представляет собой сумму функций, рассмотренных в предыдущих пунктах, то по принципу суперпозиции частное решение будет задаваться как сумма решений, соответствующих каждому из слагаемых правой части.
Пример.
Для уравнения 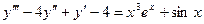 частное решение ищем в виде:
частное решение ищем в виде:
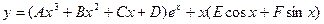 .
.
Дата добавления: 2015-03-19; просмотров: 700;
