ЛОС с постоянными коэффициентами.
Опред.: Если матрица 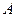 не диагонализируемая, то ее характеристическое уравнение имеет кратные корни.
не диагонализируемая, то ее характеристическое уравнение имеет кратные корни.
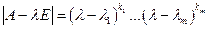
Лемма:
Пусть 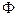 - фундаментальная матрица ЛОС
- фундаментальная матрица ЛОС 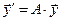 , где
, где 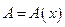 - матрица
- матрица 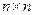 , а
, а 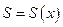 - невырожденная матрица. Тогда
- невырожденная матрица. Тогда 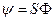 .
.
ЛОС 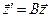 , где
, где 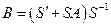
Доказательство:
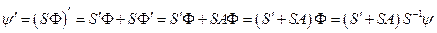
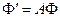
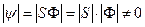
Следствие 1:
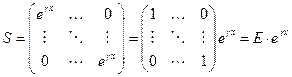
| 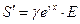
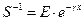
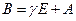
|
Вывод: собственные числа увеличатся на 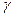 .
.
Следствие 2:
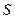 - постоянная матрица.
- постоянная матрица.
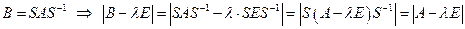
Вывод: собственные числа не изменятся.
Теорема (о структуре общего решения):
Фундаментальную систему решений линейной однородной системы 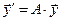 можно составить из
можно составить из 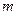 подмножеств, соответствующих попарно различным корням
подмножеств, соответствующих попарно различным корням 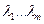 характеристического многочлена, причем корню
характеристического многочлена, причем корню 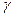 кратности
кратности 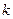 соответствует
соответствует 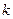 линейно независ. решений вида
линейно независ. решений вида 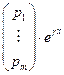 , где
, где 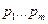 - многочлены степени не превосходящей
- многочлены степени не превосходящей 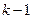 .
.
Доказательство:
Доказательство проводим индукцией по 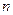 при фиксированном
при фиксированном 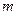 .
.
База индукции при 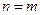
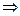 все корни (собственные числа) различны
все корни (собственные числа) различны 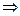 теорема справедлива.
теорема справедлива.
Шаг индукции.Предположим, что теорема справедлива для числа 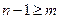 . Докажем ее для
. Докажем ее для 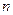 .
.
Из ограничения общности можно считать, что 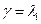 ,
, 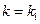 , а теорема уже доказана для случая, когда
, а теорема уже доказана для случая, когда 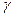 - корень кратности
- корень кратности 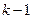 ,
, 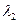 -корень кратности
-корень кратности 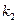 ,
, 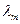 -корень кратности
-корень кратности 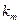 .
.
Можно считать, что 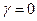 , иначе делаем замену
, иначе делаем замену 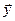 на
на 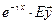 .
.
Пусть  - собственный вектор, соответствующий
- собственный вектор, соответствующий 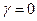 . Значит,
. Значит, 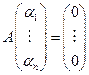 . Можно считать, что
. Можно считать, что 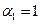 .
.
Сделаем замену переменных: 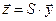 ,
, 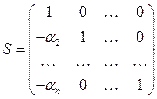 ,
, 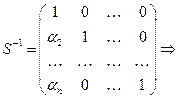
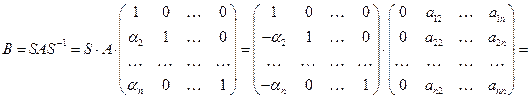
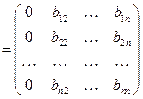 .
.
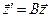 ,
,
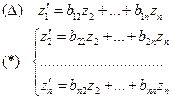
Из уравнения 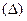 следует:
следует: 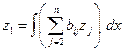
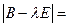
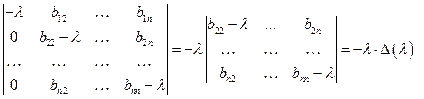
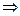
учитывая, что 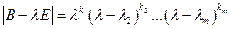 , получаем:
, получаем: 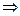
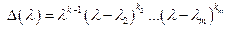 .
.
ФСР 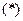 : : 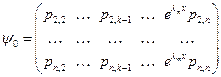
| 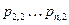 - многочлены, степени - многочлены, степени 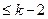
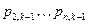 - многочлены, степени - многочлены, степени 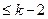
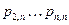 - многочлены, степени - многочлены, степени 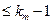
|
ФСР 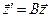
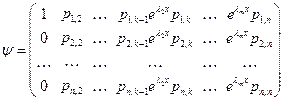
| В данной матрице 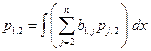 . .
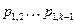 - многочлены, степени - многочлены, степени 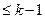
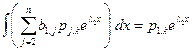 - степень - степень 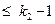
|
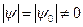 ,
, 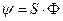 (где
(где 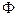 - фундаментальная матрица исходной системы).
- фундаментальная матрица исходной системы).
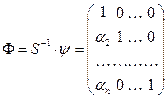 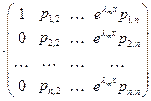
|
В результате такого произведения получим матрицу, аналогичную матрице 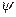 . .
|
Билет № 21
Дата добавления: 2015-01-15; просмотров: 1088;
