Линейные неоднородные ДУ 2 порядка с постоянными коэффициентами со специальной правой частью.
Рассм. ДУ
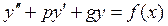
Общее решение такого уравнения:
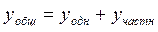 , где
, где 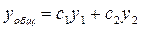
ФСР 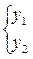 - уже рассматривали
- уже рассматривали
Укажем метод нахождения частного решения неоднородного уравнения
 , если f(x) имеет специальный вид.
, если f(x) имеет специальный вид.
 Рассмотрим следующие случаи:
Рассмотрим следующие случаи:
I. 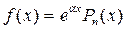 ,где
,где 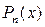 - многочлен степени n.
- многочлен степени n.
а) 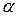 - не корень характеристического уравнения
- не корень характеристического уравнения 
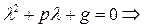
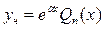 , где
, где 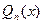 - многочлен степени n с неопределенными буквенными коэффициентами. Подставим
- многочлен степени n с неопределенными буквенными коэффициентами. Подставим 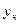 в ДУ и сравнив коэффициенты при одинаковых степенях найдём все буквы.
в ДУ и сравнив коэффициенты при одинаковых степенях найдём все буквы.
б) 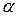 - корень характеристического уравнения кратности 1
- корень характеристического уравнения кратности 1 
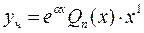
в) 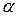 - корень характеристического уравнения кратности 2
- корень характеристического уравнения кратности 2 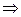
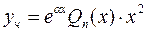
II. . 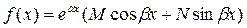 ,где M,Nчисла
,где M,Nчисла
a) 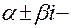 не корень характеристического уравнения
не корень характеристического уравнения 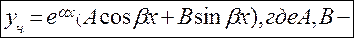 неопределенные коэффициенты.Подставив
неопределенные коэффициенты.Подставив 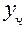 в ДУ и приравняв коэффициенты при
в ДУ и приравняв коэффициенты при 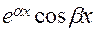
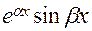 находим А и В
находим А и В
б) 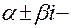 корень характеристического уравнения кратности 1
корень характеристического уравнения кратности 1 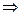
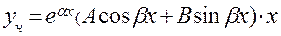
|
Замечание : Если в правой части 
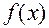 есть только
есть только 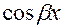 или
или 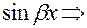
в частном решении 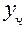 должны быть и sin и cos , т.е тригонометрия должна быть полной.
должны быть и sin и cos , т.е тригонометрия должна быть полной.
III. . 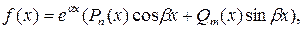
Где 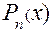 ,
, 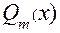 -многочлены степеней m и n
-многочлены степеней m и n
a) 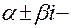 не корень характеристического уравнения
не корень характеристического уравнения 
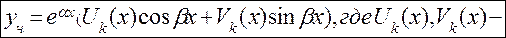 многочлены степени к с неопределенными коэффициентами
многочлены степени к с неопределенными коэффициентами
б) 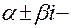 корень характеристического уравнения
корень характеристического уравнения 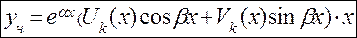
Дата добавления: 2015-01-09; просмотров: 1161;
