Линейные однородные дифференциальные уравнения 2 порядка с постоянными коэффициентами
 Это уравнения вида:
Это уравнения вида: 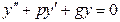 , где p и g – числа(*)
, где p и g – числа(*)
Определение:Уравнение 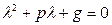 - называется характеристическим уравнением дифференциального уравнения (*) – обычное квадратное уравнение, решение которого зависит от D, возможны следующие случаи:
- называется характеристическим уравнением дифференциального уравнения (*) – обычное квадратное уравнение, решение которого зависит от D, возможны следующие случаи:
1)D>0 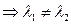 - два действительных различных решения.
- два действительных различных решения.
2)D=0 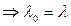 - один действительный корень кратности 2.
- один действительный корень кратности 2.
3)D<0 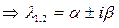 - два комплексно сопряжённых корня.
- два комплексно сопряжённых корня.
Для каждого из этих случаев укажем фундаментальную систему решений, составленную из 2 функций 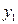 и
и 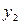 .
.
Будем показывать что:
1) 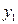 и
и 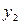 - ЛНЗ
- ЛНЗ
2) 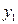 и
и 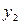 - решение (*)
- решение (*)
Рассмотрим 1 случай D>0 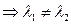 - 2 действительных различных корня.
- 2 действительных различных корня.
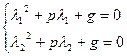 Характеристическое уравнение:
Характеристическое уравнение: 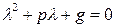
В качестве ФСР возьмём: 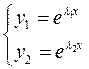
а) покажем ЛНЗ 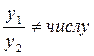
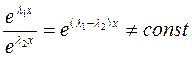
б) покажем, что 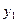 - решение (*), подставим
- решение (*), подставим 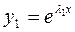
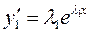
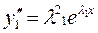
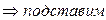
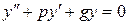
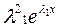 + p
+ p 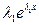 +g
+g 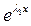 =0
=0
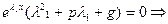 верное равенство
верное равенство 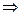
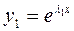 решение (*)
решение (*)
аналогично показывается для y2.
 Вывод:
Вывод: 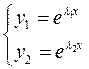 - ФСР (*)
- ФСР (*) 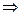 общее решение
общее решение 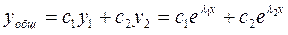
Рассмотрим 2случай: D=0 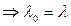 - 1 действительный корень кратности 2.
- 1 действительный корень кратности 2.
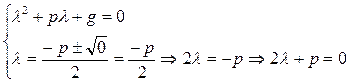
В качестве ФСР возьмём: 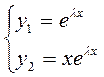
ЛНЗ: 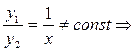 ЛНЗ есть.
ЛНЗ есть.
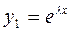 - решение уравнения (см. 1 случай). Покажем что
- решение уравнения (см. 1 случай). Покажем что 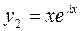 - решение.
- решение.
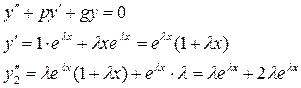
подставим в ДУ
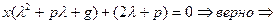
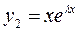 - решение.
- решение.
Вывод:ФСР 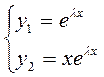

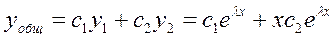
Пример: 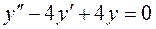
3 случай:D<0 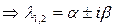 - 2 комплексно сопряжённых корня.
- 2 комплексно сопряжённых корня.
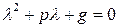
подставим 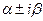 в характ. уравнение
в характ. уравнение
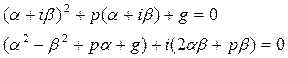
 комплексное число равно 0, когда действительная и мнимая часть равны 0.
комплексное число равно 0, когда действительная и мнимая часть равны 0.
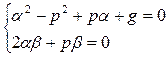 - будем использовать.
- будем использовать.
Покажем, что 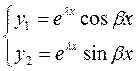 - образуют ФСР.
- образуют ФСР.
А)ЛНЗ: 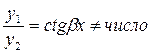
Б) 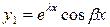 - решение ДУ
- решение ДУ 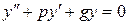
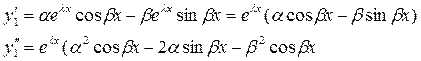
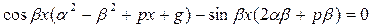
верное равенство 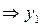 - решение ДУ.
- решение ДУ.
Аналогично показывается, что 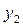 тоже решение.
тоже решение.
 Вывод:ФСР:
Вывод:ФСР: 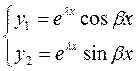
Общее решение: 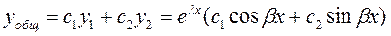
Пример:
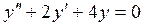
Если заданы н.у.
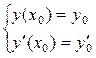 - то сначала находят общее решение
- то сначала находят общее решение 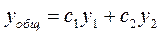 , его производную:
, его производную: 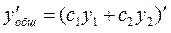 , а потом в эту систему подставляют н.у и находят
, а потом в эту систему подставляют н.у и находят 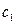 и
и 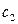 .
.
Пример:
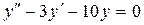 Н.у:
Н.у: 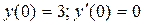
Дата добавления: 2015-01-09; просмотров: 988;
