Линейные однородные ДУ порядка n с постоянными коэффициентами
Это уравнения вида: 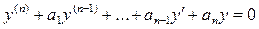 , где аi – числа.
, где аi – числа.
Характеристическое уравнение будет иметь вид: 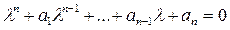
Слева стоит многочлен степени n, который имеет n корней с учётом их кратности и комплексности, следовательно, ФСР будет состоять из n решений:
1) Каждому простому корню характеристического уравнения 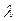 , (имеющему кратность 1) ставится в соответствие
, (имеющему кратность 1) ставится в соответствие 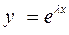
2)Каждому действительному корню 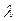 кратности r ставится в соответствие r решений:
кратности r ставится в соответствие r решений:
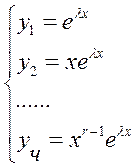
3) Каждой паре комплексно сопряжённых корней 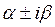
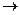 2 фундаментальных решения:
2 фундаментальных решения: 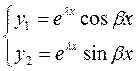
4) Если пара комплексно сопряжённых корней 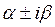 имеет кратность 2 и выше, то ФСР строятся аналогично 2 случаю.
имеет кратность 2 и выше, то ФСР строятся аналогично 2 случаю.
 Общее решение уравнения – линейная комбинация фундаментальных решений
Общее решение уравнения – линейная комбинация фундаментальных решений 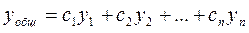
Основная трудность состоит в том, чтобы правильно решить характеристическое уравнение.
Пример: 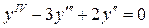
Дата добавления: 2015-01-09; просмотров: 902;
