Аналитическое выравнивание по параболе второго порядка
Если изучаемый динамический ряд характеризуется положительными абсолютными приростами, с ускорением развития уровней, то выравнивание ряда может быть проведено по параболе второго порядка.
По ней рассчитывают теоретические траектории движения артиллерийских снарядов, баллистических ракет, искусственных спутников и др.
Уравнение параболы второго порядка имеет следующий вид:
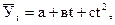 (9.31)
(9.31)
где: 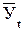 – выровненное значение уровней динамического ряда; t – периоды или моменты времени, к которым относятся уровни; а, в, с – параметры уравнения (искомой параболы), которые следует определить.
– выровненное значение уровней динамического ряда; t – периоды или моменты времени, к которым относятся уровни; а, в, с – параметры уравнения (искомой параболы), которые следует определить.
Положив в основу вычисления параметров а, в, с способ наименьших квадратов, получим следующую систему нормальных уравнений:
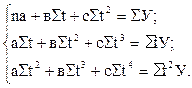
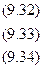
Приняв срединный уровень ряда условно за начальный, будем иметь Σt=0; Σt3=0, а систему уравнений можно привести к упрощенному виду:
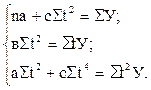
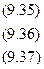
Из этих уравнений можно найти параметры а, в, с, которые в общем виде выразятся следующим образом:
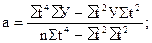
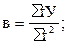
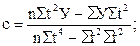
Отсюда видно, что для определения параметров а, в, с необходимо рассчитать следующие значения: 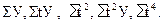
Выравнивание динамического ряда по параболе второго порядка покажем на примере изменения объема травяной муки (табл. 9.11).
Т а б л и ц а 9.11.Аналитическое выравнивание поставки травяной
муки на комбикормовый завод «Неман»
| Годы | Поставка, т (У) | Расчет величины | Выравненный ряд, т (У) | ||||
| t | t2 | t4 | tУ | t2У | |||
| -2 | -704 | 340,4 | |||||
| -1 | -369 | 375,6 | |||||
| 455,5 | |||||||
| 530,5 | |||||||
| 750,0 | |||||||
| Итого |
Установив значения расчетных величин (табл. 9.11), переходят к определению параметров а, в, с уравнения параболы второго порядка (9.31):
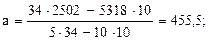
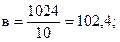
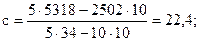
Теперь по полученному уравнению параболы второго порядка, имеющему вид 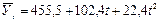 , определим значения выравненных уровней динамического ряда для каждого года; например,
, определим значения выравненных уровней динамического ряда для каждого года; например,
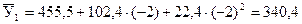 т;
т;
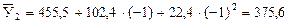 т;
т;
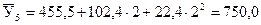 т.
т.
Полученные результаты заносим в последний столбец табл. 9.11.
Выравненные уровни более четко отражают основную тенденцию изменения объема травяной муки, поставляемой комбикормовому заводу.
Дата добавления: 2015-02-16; просмотров: 1987;
