Теорема Ляпунова.

Теорема:

Пусть нормальная система 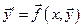имеет решение 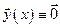. Пусть существует дифференцируемая функция 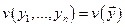, удовлетворяющая условиям:

1). , .

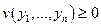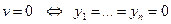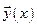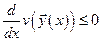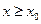2). если - решение, то при , тогда точка покоя 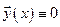устойчива по Ляпунову.

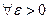
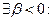
Если к тому же 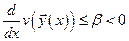при 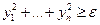, , 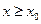то точка покоя 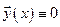асимптотически устойчива.

Опред.:Функция 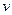называется функцией Ляпунова.

Следствие:

Если действительные части всех собственных чисел матрицы 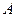отрицательны, то любое решение 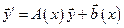ассимптотически устойчиво.

Доказательство:

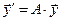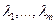, - собственные числа матрицы .

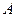Если , .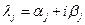

.

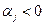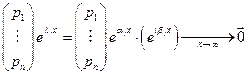Билет № 23