Свойства собственного значения и собственной функции.

1. Существует монотонной возрастающая последовательность собственных значений 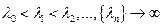, причем 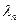соответствует собственная функция 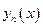, обращающаяся в ноль ровно 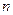раз на .

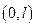2.Если 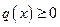, то все собственные значения положительны, за исключением случая , , , .

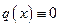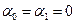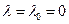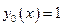3. Собственные функции на отрезке 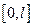образуют ортонормированную систему с весом 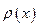, то есть 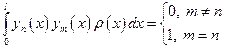(теорема Стеклова).

4. Всякая функция 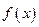, удовлетворяющая краевым условиям и имеющая непрерывную 1-ю производную и кусочно-непрерывную 2-ю производную, разлагается в абсолютно и равномерно сходящийся ряд по собственным функциям :

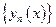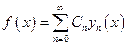, где .

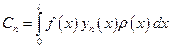Пример:

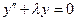
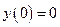
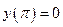
Характеристические корни: .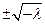

1). ,

.

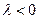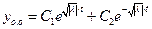
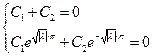
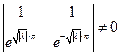
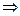
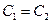2). .

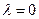
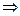
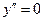
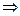
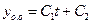
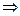
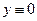3).

; , ;

( , , )

,

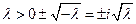
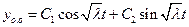
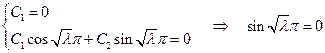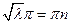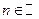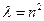
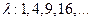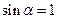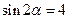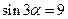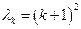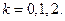
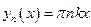
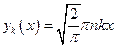- орт. на .

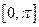Билет № 26