Локальная и интегральная теорема Муавра-Лапласа

Локальная теорема.Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна р (0 < р <1), событие наступит ровно m раз (безразлично, в какой последовательности), приближенно равна (тем точнее, чем больше n)

Здесь

, ,

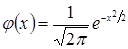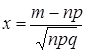Таблица значений функции Гаусса 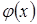для положительных значений х приведена в приложении 1; для отрицательных значений х пользуются этой же таблицей с учетом того, что функция 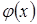четная, следовательно, .

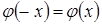Интегральная теорема.Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна р (0 < р < 1), событие наступит не менее m₁ раз и не более m₂ раз, приближенно равна

P(m₁; m₂) = Φ(x¢¢) – Φ(x¢)

Здесь – функция Лапласа,

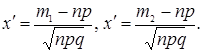
Таблица значений функции Лапласа для положительных значений х (0 ≤ х ≤ 5) приведена в приложении 2; для значений х > 5 полагают Φ(x) = 0,5. Для отрицательных значений х используют эту же таблицу, учитывая, что функция Лапласа нечетная Ф(–x)= –Ф(x).

На практике, приближенные равенства из локальной и интегральной теоремы Муавра-Лапласа используют при выполнении условия: npq > 20.