Числовые характеристики дискретных случайных величин
Характеристикой среднего значения случайной величины служит математическое ожидание.
Математическим ожиданием дискретной случайной величины называют сумму произведений всех ее возможных значений на соответствующие им вероятности:
М(X) = x1p1+ x1p2+…+ xnpn.
Характеристиками рассеяния возможных значений случайной величины вокруг математического ожидания являются дисперсия и среднее квадратическое отклонение.
Дисперсией случайной величины X называют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:
D(X) = M[X – M(X)]2.
Дисперсию удобно вычислять по формуле
D(Х) = М(X2) – [М(Х)]2.
Средним квадратическим отклонением случайной величины называют квадратный корень из дисперсии:
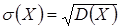 .
.
Дата добавления: 2015-03-26; просмотров: 841;
