Дифференциальная функция распределения
Плотностью распределения вероятностей непрерывной случайной величины называют первую производную от функции распределения:
f(х) = F¢(х).
Часто вместо термина «плотность распределения» используют термины «плотность вероятностей» или «дифференциальная функция».
Вероятность того, что непрерывная случайная величина X примет значение, принадлежащее интервалу (a, b),определяется равенством:
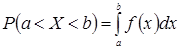 .
.
Зная плотность распределения, можно найти функцию распределения:
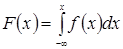 .
.
Плотность распределения обладает следующими свойствами:
Свойство 1.Плотность распределения неотрицательна, т.е. f(x)≥0.
Свойство 2. 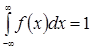 . В частности, если все возможные значения случайной величины принадлежат интервалу (а, b), то
. В частности, если все возможные значения случайной величины принадлежат интервалу (а, b), то 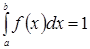 .
.
Дата добавления: 2015-03-26; просмотров: 819;
