Числовые характеристики непрерывных случайных величин
Математическое ожидание непрерывной случайной величины Х, возможные значения которой принадлежат всей оси Ox, определяется равенством
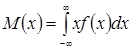 ,
,
где f(x) – плотность распределения случайной величины X. Предполагается, что интеграл сходится абсолютно.
В частности, если все возможные значения принадлежат интервалу
(а, b), то
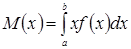 .
.
Дисперсия непрерывной случайной величины X, возможные значения которой принадлежат всей оси Ох, определяется равенством
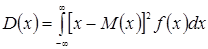 ,
,
или равносильным равенством
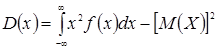 .
.
В частности, если все возможные значения X принадлежат интервалу (a, b), то
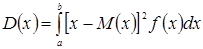 .
.
Среднее квадратическое отклонение непрерывной случайной величины определяется так же, как и для дискретной величины:
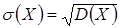 .
.
Дата добавления: 2015-03-26; просмотров: 794;
