Параграф 4. Теорема об изменении количества движения МТ
Основной закон динамики (1.1) можно представить в виде:
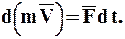 (1.29)
(1.29)
Здесь 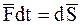 – элементарный импульс силы, действующей на МТ.
– элементарный импульс силы, действующей на МТ.
Соотношение (1.29) выражает теорему об изменении количества движения МТ в дифференциальной форме.
Теорема: Дифференциал количества движения МТ равен элементарному импульсу силы, действующей на МТ.
Проинтегрировав соотношение (1.29) с учетом начальных условий: при t = 0  , получим эту теорему в конечной интегральной форме:
, получим эту теорему в конечной интегральной форме:
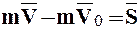 . (1.30)
. (1.30)
В (1.30) 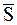 называется импульсом силы за конечный промежуток времени:
называется импульсом силы за конечный промежуток времени:
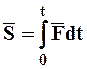 . (1.31)
. (1.31)
Теорема: Изменение количества движения МТ за конечный промежуток времени равно импульсу силы, действующей на МТ за тот же промежуток времени.
Проектируя на оси декартовой системы координат равенство (1.30), получим эту теорему в скалярной форме:
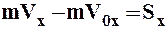 ,
,
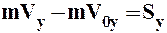 , (1.32)
, (1.32)
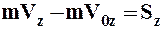 ,
,
Дата добавления: 2015-01-13; просмотров: 864;
