Метод вариации постоянных.

Данный метод позволяет найти частное решение.

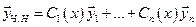
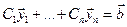
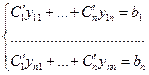
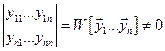
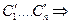находим 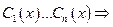находим .

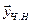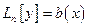
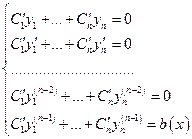
Находим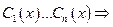

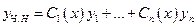
Билет № 16

3°. ЛОУ 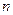-го порядка с постоянными коэффициентами.

, .

,

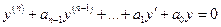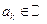
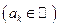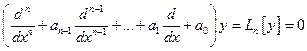
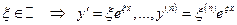
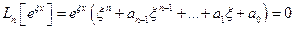
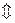
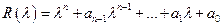(характеристический многочлен).

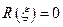
Пусть 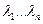- все корни характеристического многочлена .

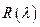1-й случай ( 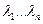различны):

Тогда 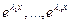- ФСР.

, .

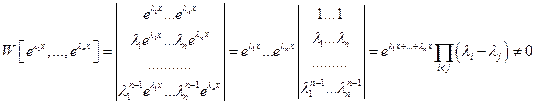
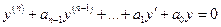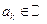
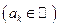Пусть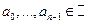

Если 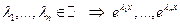- действительны и являются ФСР.

Если ,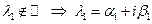

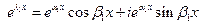
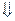
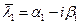- корень ,

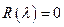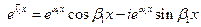
Следовательно 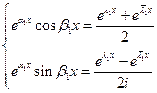- решения .

,

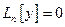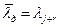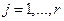
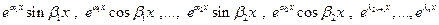- линейно независимы

над 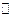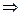линейно независимы над .

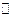Билет № 17

3°. ЛОУ 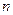-го порядка с постоянными коэффициентами.

, .

,

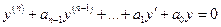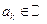
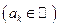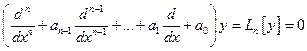
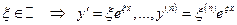
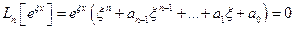
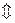
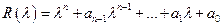(характеристический многочлен).

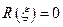
Пусть 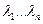- все корни характеристического многочлена .

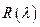2-й случай (среди 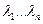есть одинаковые):

Лемма 1:

Если 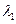- корень кратности 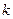характеристического многочлена 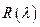, то

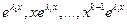
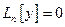, линейно независимы над .

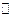Доказательство:

{

}

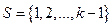
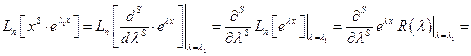
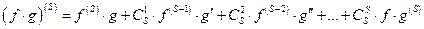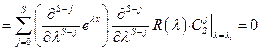
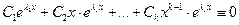
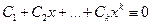
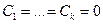
Лемма доказана.

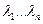- различные среди корней характеристического многочлена с кратностями ,

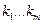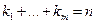
Лемма 2:

Если , где 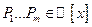- многочлены с комплексными коэффициентами.

.

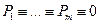Доказательство (проводим индукцией по ):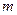

База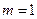

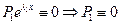
Шаг 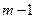- л. справа.

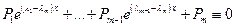
Продифференцируем это равенство 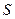раз:

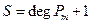
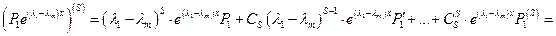
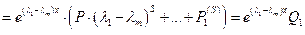
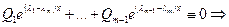
Теорема:

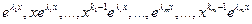- ФСР .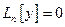

Доказательство:

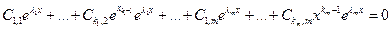
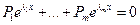
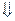
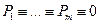
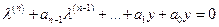
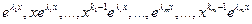
Пусть ,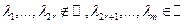

,

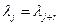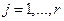
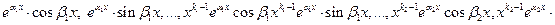
Линейно независимо над 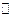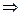линейно независимо над .

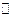Билет № 18

4°. Линейные неоднородные уравнения 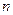- го порядка с постоянными коэффициентами и правой частью.

, , .

,

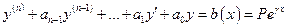
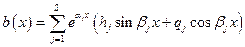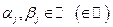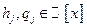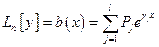, где , .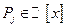

,

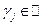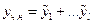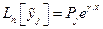
Теорема:

Если 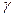- корень кратности 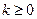характеристического многочлена 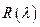, то частное решение уравнения 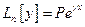можно искать в ви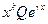де , где , .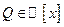

Доказательство:

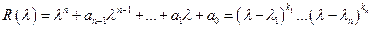
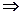
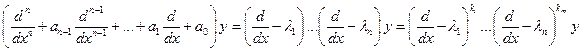
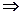
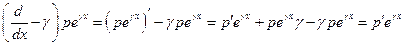
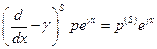
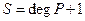
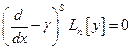
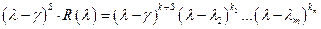
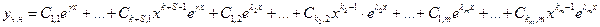
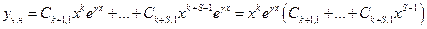
Билет № 19