Определитель Вронского (Вронскиниан).
Опред.:Определителем Вронского вектор-функций 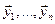 называется определитель
называется определитель
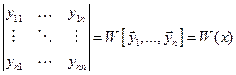
Решения 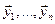 (ЛОС) образуют ФСР тогда и только тогда, когда
(ЛОС) образуют ФСР тогда и только тогда, когда 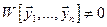 (хотя бы в одной точке).
(хотя бы в одной точке).
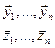 - ФСР
- ФСР 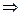
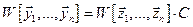 ,
, 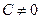 .
.
Билет № 11
5°. Линейные однородные дифференциальные уравнения 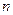 -го порядка.
-го порядка.
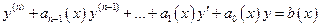 - ЛДУ
- ЛДУ
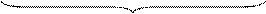
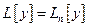 - линейный дифференциальный оператор
- линейный дифференциальный оператор 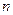 -го порядка.
-го порядка.
Если 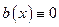 , то получаем линейное однородное дифференциальное уравнение (ЛОДУ)
, то получаем линейное однородное дифференциальное уравнение (ЛОДУ)
Если 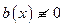 , то получаем линейное неоднородное дифференциальное уравнение
, то получаем линейное неоднородное дифференциальное уравнение
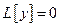
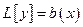
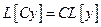
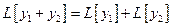
Сумма решений ОДУ 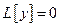 , а также произведение решения на число снова является решением.
, а также произведение решения на число снова является решением.
Уравнению 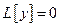 можно поставить в соответствие линейную однородную систему:
можно поставить в соответствие линейную однородную систему:
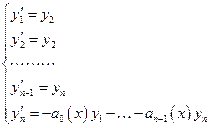
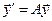
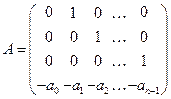
Каждому решению 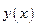 уравнения
уравнения 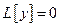 можно однозначно сопоставить решение
можно однозначно сопоставить решение
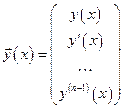 ЛОС
ЛОС 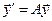
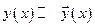 (1)
(1)
Соответствие (1) не нарушается при сложении решений и умножении решения на число. Оно также сохраняет линейную зависимость или независимость решений.
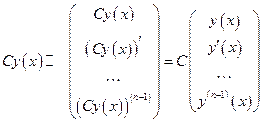
| 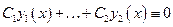 на на 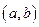
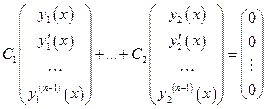
|
Свойства уравнения 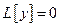 :
:
1. Если 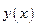 - решение уравнения
- решение уравнения 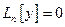 на
на 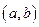 и
и 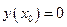 ,
, 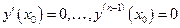 , то
, то 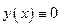 на
на 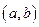 .
.
2. Множество всех решений уравнения 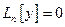 является линейным пространством размерности
является линейным пространством размерности 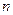 .
.
3. Решения 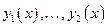 уравнения
уравнения 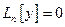 линейно независимы тогда и только тогда, когда они линейно независимы хотя бы при одном значении
линейно независимы тогда и только тогда, когда они линейно независимы хотя бы при одном значении 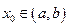 .
.
ФСР называется любой базис пространства решений, то есть любые 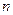 линейно независимых решений.
линейно независимых решений.
4. Теорема о структуре общего решения:
Если функции 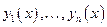 образуют ФСР, то функция
образуют ФСР, то функция 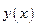 является решением тогда и только тогда, когда
является решением тогда и только тогда, когда 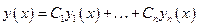 , где
, где 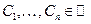 .
.
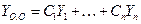
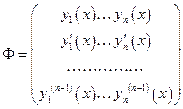 - фундаментальная матрица.
- фундаментальная матрица.
Опред.:Определителем Вронского функций 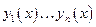 называется определитель
называется определитель
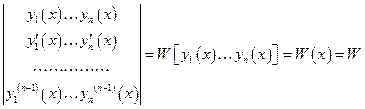
5. Решения 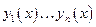 уравнения
уравнения 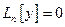 образуют ФСР тогда и только тогда, когда
образуют ФСР тогда и только тогда, когда
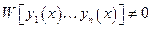
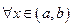 .
.
Замечание: для линейной независимости произвольных функций 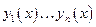 условие
условие 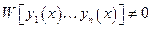 является достаточным, но не необходимым.
является достаточным, но не необходимым.
Пример:
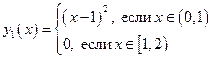
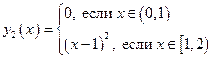
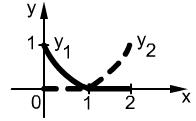
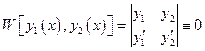 на
на 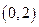
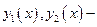 ЛНУ, так как если
ЛНУ, так как если 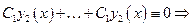
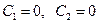
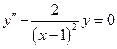
Билет №12
Дата добавления: 2015-01-15; просмотров: 1465;
