Нормальная система.

Опред.:Нормальной системой называется совокупность уравнений вида:

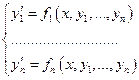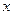, где - независимая переменная,

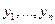- искомые функции от 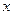, 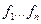- задание функции от 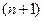переменной.

Опред.:Нормальная система называется автономной (стационарной), если функции 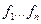не зависят явно от 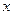, и неавтономной в противном случае.

Опред.:Решением нормальной системы на интервале 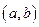называется совокупность функций 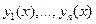, определенных на интервале 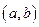, при подстановки которых все уравнения этой системы обращаются в тождества 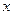на интервале .

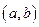Опред.:Первым интегралом нормальной системы называется равенство 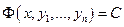, если оно выполняется для любого решения системы при соответствующем значении .

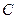Опред.:Задачей Коши для нормальной системы называется задача нахождения решения 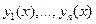этой системы, удовлетворяющего его условиям 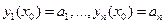(начальное условие).

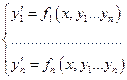
3°. Связь нормальных систем с общими дифференциальными уравнениями (ОДУ) n-го порядка.

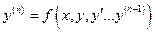
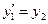
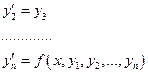
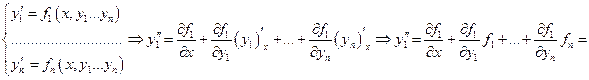
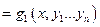
Исключим из этих уравнений переменные 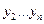. Тогда у нас останется уравнение, которое получается методом подстановки.

Подставим в последнее уравнение вместо переменных 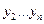их выражение через переменные

: .

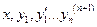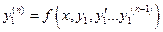Теорема (о существовании и единственности решения нормальной системы):

Пусть функции 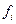и их частные производные 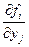, 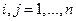непрерывны в некоторой области 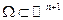(расширенное фазовое пространство). Тогда для каждой точки 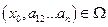существует отрезок 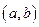, такой что 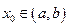и единственное решение нормальной системы

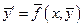, определенное на 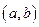, удовлетворяющее условиям .

Доказательство:

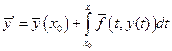(при интегрировании ).

.

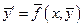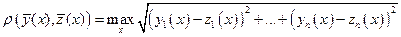Следствие (для дифференциальных уравнений 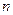- ного порядка):

Пусть правая часть дифференциального уравнения 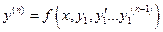и её частные производные 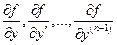непрерывны в некоторой области 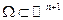. Тогда для любой точки 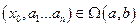существует интервал 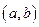, такой что 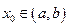и единственное решение дифференциального уравнения, определенное на 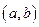и удовлетворяющее условиям .

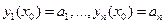Опред.:Решение дифференциального уравнения - это функция от 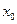, это точка.