Теорема о существовании и единственности решения дифференциального уравнения 1-го порядка.
Теорема.
 Пусть функция
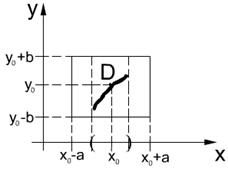
Пусть функция 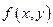 непрерывна в прямоугольнике
непрерывна в прямоугольнике 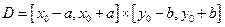 , причем
, причем 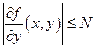 в
в 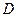 . Тогда на интервале
. Тогда на интервале 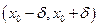 , где
, где 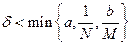
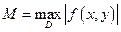 , существует и единственно решение дифференциального уравнения
, существует и единственно решение дифференциального уравнения 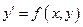 , удовлетворяющее условию
, удовлетворяющее условию 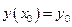 .
.
Поставленная задача Коши эквивалентна решению интегрального уравнения.
Доказательство.
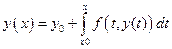 на
на 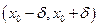 .
.
 .
. 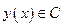
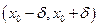 ,
, 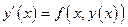 на
на 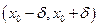 ,
, 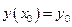
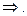
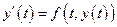 .
.
Проинтегрируем это равенство на отрезке 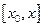 :
: 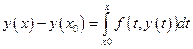 .
.
Рассмотрим произвольный отрезок 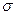 :
: 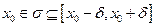
Рассмотрим метрическое пространство M, состоящее из непрерывных функций на отрезке 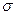 и удовлетворяющих неравенству:
и удовлетворяющих неравенству: 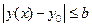 на
на 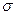 , M
, M 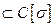
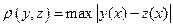
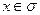
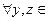 M.
M.
Рассмотрим произвольную фундаментальную последовательность 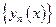 - худ. из M.
- худ. из M.
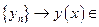
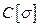
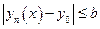
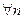 ,
, 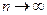
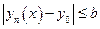
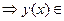 M
M
Рассмотрим на пространстве Mсжимающий оператор 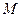 :
: 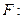 M
M 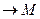 .
.
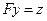 ,
, 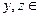 M
M 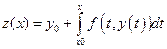
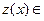
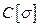
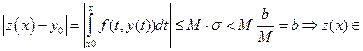 M.
M.
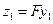 ,
, 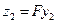
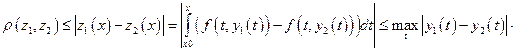
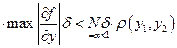
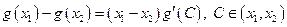
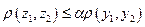
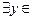 M,
M, 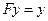
Элемент 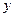 является функцией, удовлетворяющей интегральному уравнению и следовательно исходной задаче Коши.
является функцией, удовлетворяющей интегральному уравнению и следовательно исходной задаче Коши.
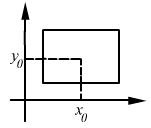
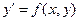
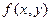 - непрерывна в
- непрерывна в 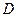
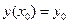
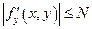
Билет № 6
Дата добавления: 2015-01-15; просмотров: 976;
