Линейно независимые и линейно зависимые системы функций. Определитель Вронского и его свойства
Определение: Система функций 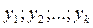 - называется линейно независимой , если линейная комбинация
- называется линейно независимой , если линейная комбинация 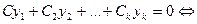 коэффициенты
коэффициенты 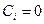 .
.
Определение:Систему функций 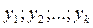 - называют линейно зависимой, если
- называют линейно зависимой, если 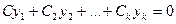 и есть коэффициенты
и есть коэффициенты 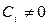 .
.
 Возьмём систему двух линейно зависимых функций
Возьмём систему двух линейно зависимых функций 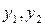 т.к
т.к 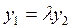 или
или 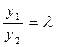 - условие линейной независимости двух функций.
- условие линейной независимости двух функций.
Примеры:
1) 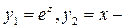 линейно независимы
линейно независимы
2) 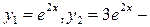 линейно зависимы
линейно зависимы
3) 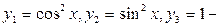 линейно зависимы
линейно зависимы
Определение:Дана система функций 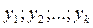 - функций переменной х.
- функций переменной х.
Определитель 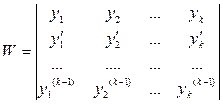 - определитель Вронского для системы функций
- определитель Вронского для системы функций 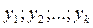 .
.
Для системы двух функций определитель Вронского выглядит следующим образом:
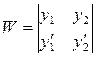
Свойства определителя Вронского:
1) Если 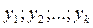 - линейно зависимы на [a;b]
- линейно зависимы на [a;b] 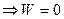 на этом отрезке.
на этом отрезке.
2) Если 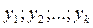 - линейно независимые, решения дифференциального уравнения
- линейно независимые, решения дифференциального уравнения 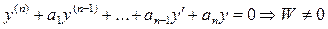 при любых значениях х в области, где определены функции а1…аn
при любых значениях х в области, где определены функции а1…аn
Теорема:Об общем решении линейного однородного дифференциального уравнения 2 порядка.
Если y1 и y2 – линейно независимые решения линейного однородного дифференциального уравнения 2 порядка, то
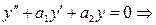 общее решение имеет вид:
общее решение имеет вид:
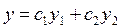
Доказательство: 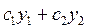 - решение по следствию из Т1 и Т2.
- решение по следствию из Т1 и Т2.
Если даны начальные условия то 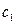 и
и 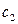 должны находится однозначно.
должны находится однозначно.
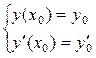 - начальные условия.
- начальные условия.
Составим систему для нахождения 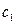 и
и 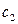 . Для этого подставим начальные условия в общее решение.
. Для этого подставим начальные условия в общее решение.
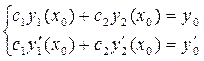
определитель этой системы: 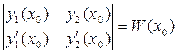 - определитель Вронского, вычисленный в точке х0
- определитель Вронского, вычисленный в точке х0
т.к 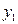 и
и 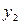 линейно независимы
линейно независимы 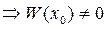 (по 20)
(по 20)
т.к определитель системы не равен 0, то система имеет единственное решение и 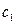 и
и 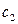 находятся из системы однозначно.
находятся из системы однозначно. 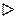
Дата добавления: 2015-01-09; просмотров: 1790;
