Системы линейных уравнений с постоянными коэффициентами, методы их решения.
Определение 23.1. Система дифференциальных уравнений называется линейной, если она линейна относительно всех неизвестных функций и их производных.
В частности, система линейных уравнений первого порядка с постоянными коэффициентами имеет вид:
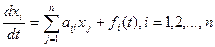. (23.1)
Можно использовать матричную запись такой системы, если ввести матрицы
. Тогда системе (23.1) эквивалентно матричное уравнение 
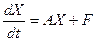. (23.2)
Если же рассмотреть линейный оператор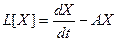 
, уравнение (23.2) примет вид:
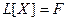. (23.3)
Так как оператор L обладает свойствами линейности:
1) L[cX] = cL[X];
2) L[X1 + X2] = L[X1] + L[X2],
то для решений линейной однородной системы (23.3) (при F = 0) справедливы те же свойства: если Х1 и Х2 – решения однородного уравнения (23.3) , то и их линейная комбинация будет решением того же уравнения.
Можно ввести понятие линейной зависимости решений Х1, Х2,…, Хп:
Определение 23.2. Векторы (столбцы) Х1, Х2,…, Хп , где
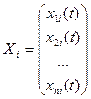, называются линейно зависимымипри 
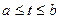, если существуют числа α1,α2,…, αп, не все равные нулю, что
α1Х1 + α2Х2 +…+ αпХп ≡ 0 (23.4)
при 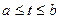. Если же тождество (23.4) справедливо только при всех αi = 0, векторы называются линейно независимыми.
Замечание. Назовем определителем Вронского для уравнения (23.4) определитель вида
, (23.5)
являющийся определителем системы уравнений, получаемых при координатной записи равенства (23.4). Можно показать, что так же, как и в случае решения линейного однородного уравнения, при W = 0 решения Х1, Х2,…, Хп линейно зависимы на [a,b]. Тогда справедлива следующая теорема:
Теорема 23.1. Линейная комбинация 
п линейно независимых решений линейной однородной системы является общим решением этой системы.
Будем искать фундаментальную систему решений линейной однородной системы с постоянными коэффициентами
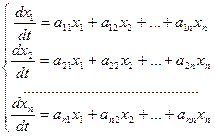(23.6)
в виде: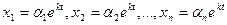 
, (23.7)
где αi – постоянные. Подставив (23.7) в (23.6) и сократив на ekt, получим:
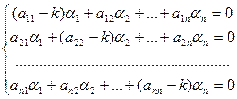. (23.8)
Для того, чтобы эта система имела ненулевое решение, необходимо и достаточно, чтобы ее главный определитель был равен нулю:
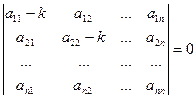, (23.9)
что представляет собой уравнение п – й степени относительно k, называемое характеристическим.
Если все корни характеристического уравнения различны, то, подставляя их последовательно в систему (23.8), можно найти соответствующие им значения 
и тем самым п различных решений системы (23.6). Эти решения линейно независимы. Действительно, если бы существовали числа β1, β2,…, βп такие, что
, то в силу линейной независимости функций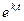 
отсюда следовало бы, что 
для каждого i. Но поскольку хотя бы одно из 
не равно нулю, получаем, что все 
. Следовательно, найденные решения (23.7) линейно независимы, и общее решение системы имеет вид: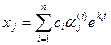 
, (23.10)
где ci – произвольные постоянные.
Пример.
. Составим характеристическое уравнение: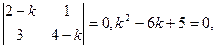 
k1 = 1, k2 =5. Для k = 1 получаем систему для определения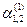 
: 
, то есть
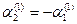. Примем 
, тогда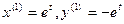 
. При k = 5 
,
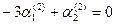. Тогда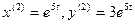 
. Следовательно, общее решение системы имеет вид: 
.
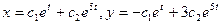В случае кратных корней характеристического уравнения решение системы (23.6) имеет вид
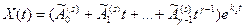, где γ – кратность корня ks.
Пример.
. Характеристическое уравнение имеет вид: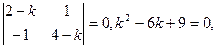 
k1 = k2 = 3. Пусть x = (c1 + c2 t)e3t, y = (c3 + c4 t)e3t. Выразим постоянные с3 и с4 через с1 и с2. Для этого подставим найденные решения в одно из уравнений системы и приравняем коэффициенты при e3t и te3t: (3c1 + c2 + 3c2t)e3t = (2c1 + c3)e3t + (2c2 + c4)te3t, c3 = c1 + c2,
c4 = c2. Итак, общее решение системы получено в форме: x = (c1 + c2 t)e3t, y = (c1+ с2 + c2t)e3t.
Замечание. Для неоднородной системы (23.1) общим решением, так же как для неоднородного уравнения, будет сумма общего решения соответствующей однородной системы и частного решения неоднородной системы. При подборе частных решений справедлив принцип суперпозиции.
Пример.
. Найдем частное решение в виде: 
. При подстановке получим: 
, откуда А = 3, В = 1. Прибавив к полученному частному решению общее решение соответствующей однородной системы, запишем общее решение исходной системы: x = c1et + 2c2e4t + 3e5t, y = -c1et + c2e4t + e5t.
Дата добавления: 2015-03-19; просмотров: 1209;