Лекция 24.

Устойчивость решений дифференциальных уравнений и их систем. Определение устойчивости по Ляпунову и асимптотической устойчивости. Автономные системы дифференциальных уравнений. Фазовое пространство (плоскость), фазовая траектория. Точки покоя. Классификация точек покоя системы двух однородных линейных дифференциальных уравнений с постоянными коэффициентами. Условия устойчивости точки покоя.

Поскольку при решении реальных задач с помощью дифференциальных уравнений начальные условия обычно являются результатами измерений и, следовательно, получены с некоторой погрешностью, очень важным является вопрос о том, как изменится решение уравнения при малом изменении начальных условий. В частности, если такие изменения существенно меняют решение, то подобное решение, очевидно, не имеет практической ценности.

Пусть некоторое явление описывается системой дифференциальных уравнений

(24.1)

с начальными условиями y_i(t₀) = y_i0 .

Определение 24.1. Решение φ_i (t) (ǐ = 1,2,…,n) называется устойчивым по Ляпунову, если

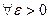
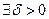такое, что для всякого решения y_i (t) той же системы, начальные условия которого удовлетворяют неравенствам 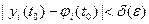, для всех 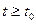справедливы неравенства 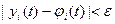(24.2)

(то есть близкие по значениям решения остаются близкими для всех ).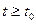

Если хотя бы для одного решения y_i (t) неравенства (24.2) не выполняются, решение φ_i (t) называется неустойчивым.

Если решение φ_i (t) не только устойчиво по Ляпунову, но и удовлетворяет условию

(24.3)

при 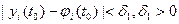, то это решение называется асимптотически устойчивым.

Замечание. Одно условие (24.3) не обеспечивает устойчивость решения.